Write an Admission Experience

Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.4

Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Solution:

According to the theorem 1, we get
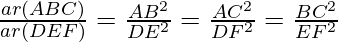
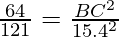
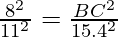
$\frac{ar(ΔABC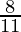)}{ar(ΔDEF)} = \frac{AB^2}{DE^2} = \frac{AC^2}{DF^2} = \frac{BC^2}{EF^2}$
$\frac{ar(ΔABC)}{ar(ΔDEF)} = \frac{BC^2}{EF^2}$
$\frac{64}{121} = \frac{BC^2}{15.4^2}$
$\frac{8^2}{11^2} = \frac{BC^2}{15.4^2}$
$\frac{8}{11} = \frac{BC}{15.4}$
BC = $\frac{8}{11}$ × 15.4
BC = 11.2 cm

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Solution:

Given, ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.
In △AOB and △COD,
∠ AOB = ∠ COD (Opposite angles)
∠ 1 = ∠ 2 (Alternate angles of parallel lines)
△AOB ~ △COD by AA property.
According to the theorem 1, we get
$\frac{ar(ΔAOB)}{ar(ΔCOD)} = \frac{AB^2}{CD^2}$
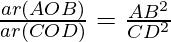
As, AB = 2CD
= $\frac{(2CD)^2}{CD^2}$
= $\frac{4CD^2}{CD^2}$
= $\frac{4}{1}$
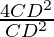
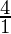
ar(AOB) : ar(COD) = 4 : 1

Question 3. In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{AO}{DO}$ .

Solution:

Let’s draw two perpendiculars AP and DM on line BC.
Area of triangle = ½ × Base × Height
$\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{½ × BC × AP}{½ × BC × DM}$
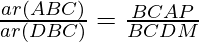
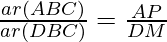$\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{AP}{DM}$ ……………………………(1)
In ΔAPO and ΔDMO,
∠APO = ∠DMO (Each 90°)
∠AOP = ∠DOM (Vertically opposite angles)
ΔAPO ~ ΔDMO by AA similarity
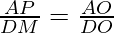$\frac{AP}{DM} = \frac{AO}{DO}$ ……………………………(2)
From (1) and (2), we can conclude that
$\mathbf{\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{AO}{DO}}$

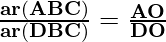
Question 4. If the areas of two similar triangles are equal, prove that they are congruent.

Solution:

As it is given, ΔABC ~ ΔDEF
According to the theorem 1, we have
$\frac{Area of (ΔABC)}{Area of (ΔDEF)} = \frac{BC^2}{EF^2}$
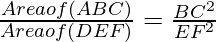
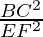$\frac{BC^2}{EF^2}$ =1 [Since, Area(ΔABC) = Area(ΔDEF)
BC² = EF²
BC = EF
Similarly, we can prove that
AB = DE and AC = DF
Thus, ΔABC ≅ ΔPQR [SSS criterion of congruence]

Question 5. D, E and F are respectively the mid-points of sides AB, BC, and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Solution:

As, it is given here
DF = ½ BC
DE = ½ AC
EF = ½ AB
So, 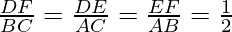$\frac{DF}{BC} = \frac{DE}{AC} = \frac{EF}{AB} = \frac{1}{2}$
Hence, ΔABC ~ ΔDEF
According to theorem 1,
$\frac{ar(ΔDEF)}{ar(ΔABC)} = \frac{DE^2}{AC^2} = \frac{EF^2}{AB^2} = \frac{DF^2}{AC^2} = \frac{1^2}{2^2}$
$\frac{ar(ΔDEF)}{ar(ΔABC)} = \frac{1}{4}$
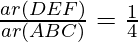
ar(ΔDEF) : ar(ΔABC) = 1 : 4

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Solution:

Given: AM and DN are the medians of triangles ABC and DEF respectively.
ΔABC ~ ΔDEF
According to theorem 1,
$\frac{ar(ΔABC)}{ar(ΔDEF)} = \frac{AB^2}{DE^2} = \frac{BC^2}{EF^2} = \frac{AC^2}{DF^2}$
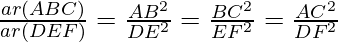
So, 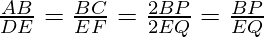$\frac{AB}{DE} = \frac{BC}{EF} = \frac{2BP}{2EQ} = \frac{BP}{EQ}$
$\frac{AB}{DE} = \frac{BP}{EQ}$ ……………………….(1)
∠B = ∠E (because ΔABC ~ ΔDEF)
Hence, ΔABP ~ ΔDEQ [SAS similarity criterion]
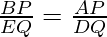$\frac{BP}{EQ} = \frac{AP}{DQ}$ ……………………….(2)
From (1) and (2), we conclude that
$\frac{ar(ΔABC)}{ar(ΔDEF)} = \frac{AP^2}{DQ^2}$
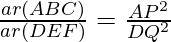
Hence, proved!

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Solution:

Let’s take side of square = a
Diagonal of square AC = a√2
As, ΔBCF and ΔACE are equilateral, so they are similar
ΔBCF ~ ΔACE
According to theorem 1,
$\frac{ar(ΔACE)}{ar(ΔBCF)} = \frac{AC^2}{BC^2}$
= $\frac{(a√2)^2}{a^2}$
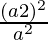
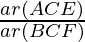$\frac{ar(ΔACE)}{ar(ΔBCF)}$ = 2
Hence, Area of (ΔBCF) = ½ Area of (ΔACE)

Tick the correct answer and justify:

Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4

Solution:

Here,
AB = BC = AC = a
and, BE = BD = ED = ½a
ΔABC ~ ΔEBD (Equilateral triangle)
According to theorem 1,
$\frac{ar(ΔABC)}{ar(ΔEBD)} = \frac{AB^2}{EB^2} = \frac{a^2}{(½a)^2}$
$\frac{ar(ΔABC)}{ar(ΔEBD)} = \frac{4}{1}$
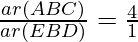
Area of (ΔABC) : Area of (ΔEBD) = 4 : 1
Hence, OPTION (C) is correct.

Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio

(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81

Solution:

ΔABC ~ ΔDEF
$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} = \frac{4}{9}$
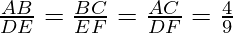
According to theorem 1,
$\frac{ar(ΔABC)}{ar(ΔDEF)} = \frac{AB^2}{DE^2}$
$\frac{ar(ΔABC)}{ar(ΔDEF)} = \frac{4^2}{9^2} = \frac{16}{81}$
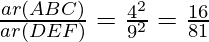
Area of (ΔABC) : Area of (ΔDEF) = 16 : 81
Hence, OPTION (D) is correct.

My Personal Notes

Last Updated : 12 Mar, 2021

Related Articles

Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.4

Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Question 3. In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{AO}{DO}$ .

Question 4. If the areas of two similar triangles are equal, prove that they are congruent.

Question 5. D, E and F are respectively the mid-points of sides AB, BC, and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Tick the correct answer and justify:

Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4

Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio

(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81

CBSE Class 12 Computer Science

GATE CS & IT 2024

Mastering System Design: From Low-Level to High-Level Solutions

Related Articles

Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.4

Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.

Question 3. In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that .

Question 4. If the areas of two similar triangles are equal, prove that they are congruent.

Question 5. D, E and F are respectively the mid-points of sides AB, BC, and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Tick the correct answer and justify:

Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4

Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio

(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81

Please Login to comment...

CBSE Class 12 Computer Science

GATE CS & IT 2024

Mastering System Design: From Low-Level to High-Level Solutions

Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Question 3. In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\frac{ar(ΔABC)}{ar(ΔDBC)} = \frac{AO}{DO}$ .