Class 10 NCERT Solutions- Chapter 2 Polynomials – Exercise 2.3
Last Updated :
03 Apr, 2024
This exercise has been deleted as per new NCERT Syllabus
Question 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2
Solution:
i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2

R = 7x-9
Q = x-3
ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x

R = 8
Q = x2+x-3
iii) p(x) = x4– 5x + 6, g(x) = 2 – x2

Q = -x2-2
R = -5x+10
Question 2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:
i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12

Q = 2t3+3t+4
R = 0
Yes 1st polynomial is factor of 2nd polynomial.
ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2

R = 0
Q = 3x2-4x+2
iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1

R = x2-1
Q = 2
Question 3. Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are and √(5/3) and -√(5/3).
Solution:
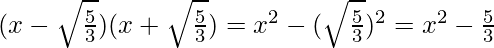

R = 0
Q = 3x2+6x+3
∴ we are factorizing
3x2+6x+3
x2+2x+1
(x+1)2
(x+1) (x+1) = 0
∴ x = -1 and x = -1
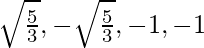
Question 4. On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:
Dividend = Divisor * Quotient + Remainder
x3-3x2+3x-2/x-2

R = 0
Q = x2 -x +1
Answer: g(x)=x2-x+1
Question 5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
i) deg p(x) = deg q(x)
p(x)=2x2-2x+14, g(x)=2
p(x)/g(x)=2x2-2x+14/2=(x2-x+7)
=x2-x+7=q(x)
=q(x)=x2-x+7
r(x)=0
ii) deg q(x)=deg r(x)
p(x)=4x2+4x+4, g(x)=x2+x+1

q(x) = 4
r(x) = 0
∴Here deg q(x)=deg r(x)
iii) deg r(x)=0
p(x)=x3+2x2-x+2 ,g(x)=x2-1

q(x) = x+2
r(x) = 4
deg of r(x) = 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...