Class 10 NCERT Solutions- Chapter 12 Areas Related to Circles – Exercise 12.3 | Set 1
Last Updated :
05 Nov, 2021
Question 1. Find the area of the shaded region in Fig., if PQ = 24 cm, PR = 7 cm and O is the center of the circle.
Solution:
In fig. By Pythagoras theorem
RQ2=RP2+PQ2
RQ2=(7)2+(24)2
RQ2=625
RQ=√625
RQ=√5*5*5*5
RQ=5*5
=25
Radius of circle =25/2cm
Areas of shaded region=Area of semi circle -Area of ∆RPQ
=1/2πR2-1/2*b*h
=(1/2*22/7*25/2)-(1/2*7*24)
=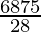 -84
-84
=161.53cm2

Question 2. Find the area of the shaded region in Fig., if radii of the two concentric circles with center O are 7 cm and 14 cm respectively and ∠AOC = 40°.
Solution:
Area of shaded Region=Area of sector AOC – Area of sector BOD
∠AOC = θ
Radius of inner circle = r
Radius of outer circle = R
=θ/360 πR2 – θ/360 πr2
= θ/360 π(R2-r2)
=40/(360)*22/7(14*14-7*7)
=40/360*22/7(196-49)
=(22/63) * 147
=154/3
=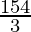 cm2
cm2

Question 3. Find the area of the shaded region in Fig., if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
Radius =14/2=7
Area of shaded region=Area of square-Area of 2 semi-circles
=side*side-2*1/2πr2
=14*14 – 22/7*7*7
=196-154
=42 cm2

Question 4. Find the area of the shaded region in Fig., where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as center.
Solution:
Area of shaded region=Area of big sector+ Area of equilateral
=θ/360 πr2+√3/4(side)2
=(300/360)*22/7*6*6+(√3/4)*12*12
=5/6*22/7*6*6+36*1.73
=660/7+62.28
=94.28+62.28
=156.56 cm2

Question 5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Figure. Find the area of the remaining portion of the square.
Solution:
radius, r = 1cm
Area of remaining poison=Area of square – Area of 4 quadrants – Area of circle in the middle
=side*side – 4(90/360 πr2) – πr2
=4*4 – 2 πr2
=16-2*22/7*1*1
=16-44/7
=9.72cm2

Question 6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Figure. Find the area of the design.
Solution:
Area of circle= πr2=22/7*32*32=22528/7=3218.28cm2 —–1
Area of ∆ABC=3*Area of ∆BOC
=3*1/2*side*side*sin120°
=3/2*32*32*sin60°
=1536*√3/2
=768*1.73
=1328.64cm2 ———2
Area of design =Area of circle – Area of ∆ABC
=321.28-1328.64
=1889.64 cm2

Question 7. In Fig., ABCD is a square of side 14 cm. With centers A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:
Area of shaded region=Area of square – Area of 4 quarters
=side*side – 4(90/360 πr2)
=14*14-22/7*7*7
=196-154
=42cm2

Question 8. Fig. here depicts a racing track whose left and right ends are semi-circular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
i) the distance around the track along its inner edge
ii) the area of the track
Solution:
i) A distance along inner edge=length of 2 parallel lines+ circumference of 2 circles
=106+106+2πr
=212+2*22/7*30
=212+188.57
=400.57m
ii) Area of track=Area of 2 rectangles+ semi rings
=106*10*2+π (R-r)2
=2120+22/7((40)2-(30)2)
=210+22/7(1600-900)
=210+2200
=4320 m2

Question 9. In Fig., AB and CD are two diameters of a circle (with center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Solution:
Area of smaller circle=πr2
=22/7*7/2*7/2
=78/2 =38.5m2
Area of segment=Area of quadrant-Area of ∆BOC
=1/4πR2-1/2*BO*OC
=1/4*22/7*7*7-1/2*7*7
=77/2-49/2
=77-49/2
=28/2
=14 cm2
Area of shaded region=Area of smaller circle+2*Area of segment
=38.5 + 2*14
=38.5+28
=66.5 cm2

Question 10. The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as center, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
Solution:
Area of equilateral ∆ =1.73205
π=3.14
√3=1.73205
√3/4 (side)2=173205
1.73205/4*(side)2=1.73205
(side)2=173205*4/1.73205
(side)2=173205*100000/10*173205
=√1000*4
=√(100 *100*2*2)
=100*2
=200cm
∴Radius of each circle=200/2=100
Area of shaded region=Area of∆ ABC-3*Area of sector
=1.73205*60/360*3.14*100*100
=1.73205-31400/2
=17320.5-15700
=1620.5cm2

Share your thoughts in the comments
Please Login to comment...