Class 10 NCERT Solutions- Chapter 1 Real Numbers – Exercise 1.4

Last Updated : 03 Apr, 2024

This exercise has been deleted as per the new NCERT syllabus

NCERT Theorem 1.5: Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form, $\frac{p}{q}$ where p and q are coprime, and the prime factorization of q is of the form 2ⁿ5^m, where n, m are non-negative integers.

NCERT Theorem 1.6: Let x = $\frac{p}{q}$ be a rational number, such that the prime factorization of q is of the form 2ⁿ5^m, where n, and m are non-negative integers. Then x has a decimal expansion which terminates.

Question 1: Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iii) $\frac{64}{455}$

(iv) $\frac{15}{1600}$

(v) $\frac{29}{343}$

(vi) $\frac{23}{2^35^2}$

(vii) $\frac{129}{2^25^77^5}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

(x) $\frac{77}{210}$

Solution:

(i) $\frac{13}{3125}$

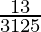
By doing prime factorization of denominator, we get

3125 = 5×5×5 = 5³

As denominator is in the form 2ⁿ5^m only where n=0 and m=3.

According to Theorem 1.6,

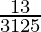$\frac{13}{3125}$ will have a terminating decimal expansion.

(ii) 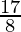$\frac{17}{8}$

By doing prime factorization of denominator, we get

8 = 2×2×2 = 2³

As denominator is in the form 2ⁿ5^m only where n=3 and m=0.

According to Theorem 1.6,

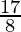$\frac{17}{8}$ will have a terminating decimal expansion.

(iii) 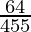$\frac{64}{455}$

By doing prime factorization of denominator, we get

455 = 5×7×13

As denominator is not in the form 2ⁿ5^m only.

According to contradiction of Theorem 1.6,

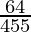$\frac{64}{455}$ will have a non-terminating decimal expansion.

(iv) 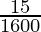$\frac{15}{1600}$

By doing prime factorization of denominator, we get

1600 = 2×2×2×2×2×2×5×5 = 2⁶5²

As denominator is in the form 2ⁿ5^m only where n=6 and m=2.

According to Theorem 1.6, 1

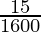$\frac{15}{1600}$ will have a terminating decimal expansion.

(v) 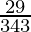$\frac{29}{343}$

By doing prime factorization of denominator, we get

343 = 7×7×7 = 7³

As denominator is not in the form 2ⁿ5^monly.

According to contradiction of Theorem 1.6,

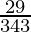$\frac{29}{343}$ will have a non-terminating decimal expansion.

(vi) 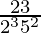$\frac{23}{2^35^2}$

Prime factorization of denominator, we have

= 2³5²

As denominator is in the form 2ⁿ5^m only where n=3 and m=2.

According to Theorem 1.6,

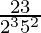$\frac{23}{2^35^2}$ will have a terminating decimal expansion.

(vii) 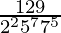$\frac{129}{2^25^77^5}$

Prime factorization of denominator, we have

= 2²5⁷7⁵

As denominator is not in the form 2ⁿ5^m only.

According to contradiction of Theorem 1.6,

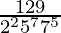$\frac{129}{2^25^77^5}$ will have a non-terminating decimal expansion.

(viii) 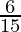$\frac{6}{15}$

$\frac{6}{15} = \frac{3}{5}$

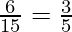
by doing prime factorization of denominator, we get

5 = 5¹

As denominator is in the form 2ⁿ5^m only where n=0 and m=1.

According to Theorem 1.6,

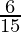$\frac{6}{15}$ will have a terminating decimal expansion.

(ix) 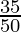$\frac{35}{50}$

by doing prime factorization of denominator, we get

50= 2×5×5 = 2¹5²

As denominator is in the form 2ⁿ5^m where n=1 and m=2.

According to Theorem 1.6,

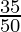$\frac{35}{50}$ will have a terminating decimal expansion.

(x) 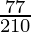$\frac{77}{210}$

by doing prime factorization of denominator, we get

210 = 2×3×5×7

As denominator is not in the form 2ⁿ5^m only.

According to contradiction of Theorem 1.6,

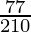$\frac{77}{210}$ will have a non-terminating decimal expansion.

Question 2: Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iv) $\frac{15}{1600}$

(vi) $\frac{23}{2^35^2}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

Solution:

(i) $\frac{13}{3125}$

= 0.00416

(ii) $\frac{17}{8}$

= 2.125

(iv) $\frac{15}{1600}$

= 0.009375

(vi) $\frac{23}{2^35^2}$

= 0.0115

(viii) $\frac{6}{15}$

= 0.4

(ix) $\frac{35}{50}$

= 0.7

Question 3: The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, $\frac{p}{q}$ what can you say about the prime factors of q?

(i) 43.123456789

(ii) 0.120120012000120000. . .

(iii) 43.123456789

Solution:

(i) 43.123456789

As this is a rational number whose decimal expansion terminates. Then it can be expressed in the form, 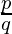$\frac{p}{q}$ where p and q are coprime, and the prime factorization of q is of the form 2ⁿ5^m, where n, m are non-negative integers.

= 43123456789 / 10⁹

= 43123456789 / 2⁹ × 5⁹

(ii) 0.120120012000120000…………..

As given decimal number expansion is non-terminating and non-repeating, then it is not a rational number. Then it can’t be expressed in the form, 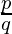$\frac{p}{q}$ where p and q are coprime, and the prime factorization of q is of the form 2ⁿ5^m, where n, m are non-negative integers.

(iii) 43.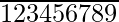 $\overline{123456789}$ [Tex] [/Tex]

As given decimal number expansion is non-terminating and repeating, then it is a rational number. Then it can be expressed in the form, 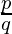$\frac{p}{q}$ where p and q are coprime, but the prime factorization of q is not in the form of 2ⁿ5^monly, where n, m are non-negative integers

Suggest improvement

Class 10 NCERT Solutions- Chapter 1 Real Numbers - Exercise 1.3

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

Share your thoughts in the comments

Chapter 1: Real Numbers

Chapter 2: Polynomials

Chapter 3: Pair of Linear Equations in Two Variables

Chapter 4: Quadratic Equations

Chapter 5: Arithmetic Progressions

Chapter 6: Triangles

Chapter 7: Coordinate Geometry

Chapter 8: Introduction to Trigonometry

Chapter 9: Some Applications of Trigonometry

Chapter 10: Circles

Chapter 11: Constructions

Chapter 12: Areas Related to Circles

Chapter 13: Surface Areas and Volumes

Chapter 14: Statistics

Chapter 15: Probability

Chapter 1: Real Numbers

Chapter 2: Polynomials

Chapter 3: Pair of Linear Equations in Two Variables

Chapter 4: Quadratic Equations

Chapter 5: Arithmetic Progressions

Chapter 6: Triangles

Chapter 7: Coordinate Geometry

Chapter 8: Introduction to Trigonometry

Chapter 9: Some Applications of Trigonometry

Chapter 10: Circles

Chapter 11: Constructions

Chapter 12: Areas Related to Circles

Chapter 13: Surface Areas and Volumes

Chapter 14: Statistics

Chapter 15: Probability

Class 10 NCERT Solutions- Chapter 1 Real Numbers – Exercise 1.4

Question 1: Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii)

(ix)

(x)

Question 2: Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

(i)

(ii)

(iv)

(vi)

(viii)

(ix)

Question 3: The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, what can you say about the prime factors of q?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iii) $\frac{64}{455}$

(iv) $\frac{15}{1600}$

(v) $\frac{29}{343}$

(vi) $\frac{23}{2^35^2}$

(vii) $\frac{129}{2^25^77^5}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

(x) $\frac{77}{210}$

(i) $\frac{13}{3125}$

(ii) $\frac{17}{8}$

(iv) $\frac{15}{1600}$

(vi) $\frac{23}{2^35^2}$

(viii) $\frac{6}{15}$

(ix) $\frac{35}{50}$

Question 3: The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, $\frac{p}{q}$ what can you say about the prime factors of q?