Circumradius of a Cyclic Quadrilateral using the length of Sides
Last Updated :
06 Apr, 2023
Given integers A, B, C, and D denoting the length of sides of a Cyclic Quadrilateral, the task is to find the circumradius i.e., the radius of circumcircle of the given cyclic quadrilateral.
Examples:
Input: A = 3, B = 4, C = 5, D= 6
Output: 3.29
Input: A = 10, B = 30, C = 50, D = 20
Output: 27.78
Approach: Follow the steps below to solve the problem:
- Calculate the semiperimeter of the cyclic quadrilateral with sides A, B, C and D by using the equation:
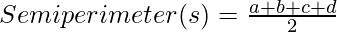
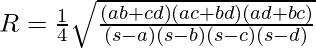

Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
double Circumradius(int a, int b, int c, int d)
{
double s = (a + b + c + d) / 2.0;
double radius = sqrt(((a * b) + (c * d)) *
((a * c) + (b * d)) *
((a * d) + (b * c)) /
((s - a) * (s - b) *
(s - c) * (s - d)));
return radius / 4;
}
int main()
{
int A = 3;
int B = 4;
int C = 5;
int D = 6;
double ans = Circumradius(A, B, C, D);
cout << setprecision(3) << ans;
return 0;
}
|
Java
import java.util.*;
class GFG{
static double Circumradius(int a, int b,
int c, int d)
{
double s = (a + b + c + d) / 2.0;
double radius = Math.sqrt(((a * b) + (c * d)) *
((a * c) + (b * d)) *
((a * d) + (b * c)) /
((s - a) * (s - b) *
(s - c) * (s - d)));
return radius / 4;
}
public static void main(String[] args)
{
int A = 3;
int B = 4;
int C = 5;
int D = 6;
double ans = Circumradius(A, B, C, D);
System.out.format("%.2f", ans);
}
}
|
Python3
import math
def Circumradius(a, b, c, d):
s = (a + b + c + d) / 2
radius = (1 / 4)*math.sqrt(((a * b)+(c * d))*
((a * c)+(b * d))*((a * d)+(b * c))
/((s-a)*(s-b)*(s-c)*(s-d)))
return radius
A = 3
B = 4
C = 5
D = 6
ans = Circumradius(A, B, C, D)
print(round(ans, 2))
|
C#
using System;
class GFG{
static double Circumradius(int a, int b,
int c, int d)
{
double s = (a + b + c + d) / 2.0;
double radius = Math.Sqrt(((a * b) + (c * d)) *
((a * c) + (b * d)) *
((a * d) + (b * c)) /
((s - a) * (s - b) *
(s - c) * (s - d)));
return radius / 4;
}
public static void Main(String[] args)
{
int A = 3;
int B = 4;
int C = 5;
int D = 6;
double ans = Circumradius(A, B, C, D);
Console.Write("{0:F2}", ans);
}
}
|
Javascript
<script>
function Circumradius(a, b, c, d)
{
var s = (a + b + c + d) / 2.0;
var radius = Math.sqrt(((a * b) + (c * d)) *
((a * c) + (b * d)) *
((a * d) + (b * c)) /
((s - a) * (s - b) *
(s - c) * (s - d)));
return radius / 4;
}
var A = 3;
var B = 4;
var C = 5;
var D = 6;
var ans = Circumradius(A, B, C, D);
document.write(ans.toFixed(2));
</script>
|
Time Complexity: O(log s)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...