Circle Theorems
Last Updated :
06 Sep, 2021
Circle is a collection of points that are at a fixed distance from a particular point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. We come across many objects in real life which are round in shape. For example, wheels of vehicles, bangles, dials of telephone, etc. In the clock also, its hands move in a round fashion repeatedly. The path traced by the tip of the hands of the clock is called a circle.
Let’s look at some terminology related to a circle in brief:
- Arc: A piece of a circle between two points is called an arc.
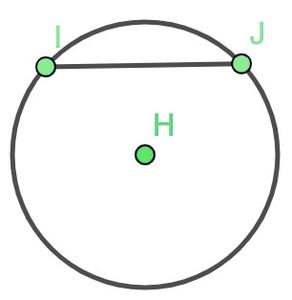
- Chord: If you take two points I and J on a circle, then the line segment IJ is called a chord of the circle.
- Circumference: The length of the complete circle is called its circumference.
- Segment: The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle.
Angle Subtended by a Chord at a Point
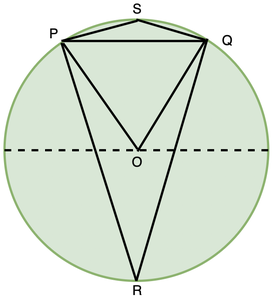
Take a chord in the figure above PQ. R and S are two points on the circle. ∠PRQ is called angle subtended by chord PQ on point R. Similarly chord subtends angles on S and also on the centre of the circle O. Let’s study the relationships between angles subtended by chord PQ on these points.
Theorem 1: Equal chords of circle subtend equal angles at the centre.
Proof:
We are given two chords KL and JI. We need to prove that ∠KHL = ∠JHI.
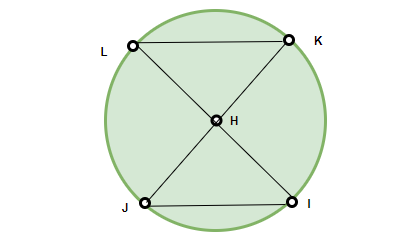
In triangles KHL and JHI,
HL = HJ
HI = HK
and we are given that KL = JI.
So, both the triangles are congruent. Thus, both of these angles are equal. Hence, proved.
Question: If ∠AOB = 50° in the figure given below, what will be the angle subtended by ∠COD, provided that the chords AB and CD are equal.
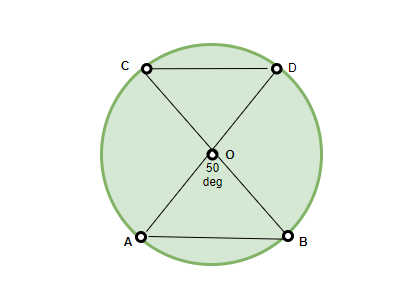
Answer:
According to the theorem mentioned above, the angles ∠AOB and ∠COD are equal, since they are equal chords subtending equal angles at the centre. Therefore, ∠COD = 50°.
Note: The converse of this theorem “If the angles subtended by two chords at the centre are equal, then the two chords are equal” is also true and can be proved similarly by the properties of triangles.
Perpendicular from the Centre to a Chord
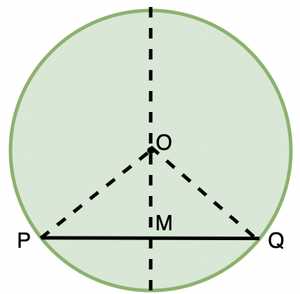
Theorem: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
Proof:
Let PQ be the chord of a circle and OM be the line from the centre that bisects the chord. Here, M is the mid point of the chord, and we have to prove that ∠OMQ = 90°.
In triangles ΔOPM and ΔOQM.
PM = MQ (perpendicular bisects the chord)
OP = OQ (radius of the circle)
OM = OM (common side of both the triangles)
So, both these triangles are congruent. This gives, angles ∠OMQ and ∠OMP as 90°
Note: The converse of this theorem “The perpendicular from the centre of a circle to a chord bisects the chord” is also true.
Angle subtended by an Arc of Circle
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Similar to the case of chords, equal arcs also subtend equal angles at the centre.
Theorem: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof:
Let’s consider three cases,
- Arc PQ is major arc.
- Arc PQ is minor arc.
- Arc PQ is semi-circle.
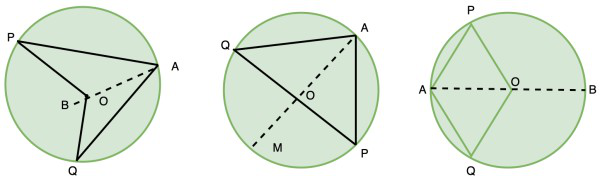
Let’s join AO and extend it to B.
In all three cases, ∠BOQ = ∠OAQ + ∠OQA. (Exterior angle of a triangle is equal to the sum of the two interior opposite angles).
Also in triangle ΔOAQ,
OA = OQ (Radii of Circle)
Therefore, ∠ OAQ = ∠ OQA
this gives, ∠ BOQ = 2∠OAQ
∠ BOP = 2∠OAP
from (1) and (2), ∠ BOP + ∠ BOQ = 2(∠ OAP + ∠ OAQ)
∠POQ = 2 ∠PAQ
For the case (iii), where PQ is the major arc, (3) is replaced by
Reflex angle POQ = 2∠PAQ
Question: What is the value of ∠ABC?
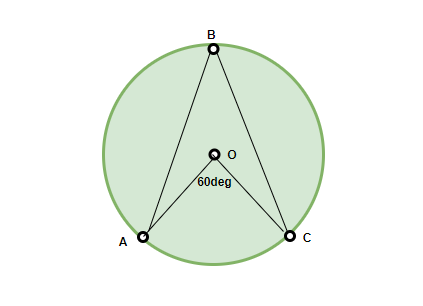
Answer:
According to the theorem, ∠AOC = 2 ∠ABC
Therefore, ∠ABC = 60°/2 = 30°
Some other properties:
- Angles in the same segment of a circle are equal.
- If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
Cyclic Quadrilaterals
A quadrilateral is called cyclic if all the four vertices of it lie on a circle.
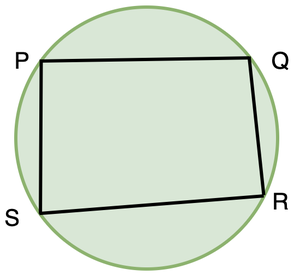
They are also called inscribed quadrilaterals.
Theorem: The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
Proof:
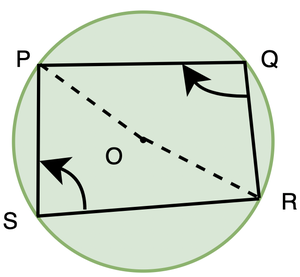
Considering arc PQR, ∠POR = 2 ∠PSR,
Similarly, considering PSR, reflex ∠POR = 2∠PQR
We know, ∠POR + reflex ∠POR = 360°.
⇒ 2 ∠PSR + 2∠PQR = 360°
⇒ 2(∠PSR + ∠PQR) = 360°
⇒ ∠PSR + ∠PQR = 180°
Thus, sum of opposite angles of cyclic quadrilateral is 180°.
Question: In the figure below, BC is the diameter of the circle, ED is a chord equal to the radius of the circle. BE and CD when extended intersect at a point F. Prove that ∠BFC = 60°.
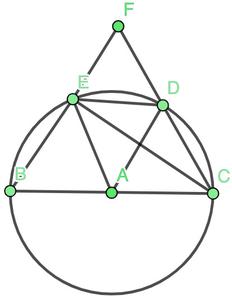
Solution:
In the figure, join AE, AD and EC. Triangle AED is an equilateral triangle.
Therefore, ∠EAD = 60o. Now, ∠ECD becomes 30o.
We know that ∠BEC = 90o.
So, by the property of exterior angles of triangle,
∠BEC = ∠ECD + ∠BFC,
90o = 30o + ∠BFC
⇒60o = ∠BFC
Hence, Proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...