Check whether two straight lines are parallel or not

Given equations of two lines (a1, b1, c1) and (a2, b2, c2) such that (ai, bi, ci) are the coefficients of X², X and a constant term of the straight line respectively, in the general equation 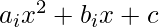, the task is to check if both the straight lines are parallel or not. If they are found to be parallel, then print “Yes”. Otherwise, print “No”.

Examples:

Input: a1 = -2, b1 = 4, a2 = -6, b2 = 12
Output: Yes
Explanation:
The slope of both lines are equal i.e., a1/b1 = a2/ b2 = -2.

Input: a1 = 11, b1 = 3, a2 = 7, b2 = -10
Output: No
Explanation: 
The slope of both lines are not equal i.e., a1/b1? a2/b2.

Approach: To check if two lines are parallel to each other or not, the idea is to compare the slope of the given lines. If the slope of the given lines is equal then the given lines are parallel. Therefore, print “Yes” else print “No”.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to check if two lines
// are parallel or not
void parallel(float a1, float b1,
              float c1, float a2,
              float b2, float c2)
{
    // If slopes are equal
    // then -(a1 / b1) = -(a2 / b2)
    // which is a1*b2 = a2*b1
    if (a1*b2 == a2*b1) {
        cout << "Yes";
    }
    else {
        cout << "No";
    }
}

// Driver Code
int main()
{
    float a1 = -2, b1 = 4, c1 = 5;
    float a2 = -6, b2 = 12, c2 = 6;

    // Function Call
    parallel(a1, b1, c1, a2, b2, c2);

    return 0;
}

Java

// Java program to implement
// the above approach
import java.util.*;
class GFG
{

// Function to check if two lines
// are parallel or not
static void parallel(float a1, float b1,
              float c1, float a2,
              float b2, float c2)
{

    // If slopes are equal
    // then (-(a1 / b1)) == (-(a2 / b2))
    // which is a1*b2 = a2*b1
    if (a1*b2 == a2*b1)
    {
        System.out.println("Yes");
    }
    else
    {
         System.out.println("No");
    }
}

// Driver Code
public static void main(String args[])
{
    float a1 = -2, b1 = 4, c1 = 5;
    float a2 = -6, b2 = 12, c2 = 6;

    // Function Call
    parallel(a1, b1, c1, a2, b2, c2);
}
}

// This code is contributed by splevel62.

Python3

# Python program to implement
# the above approach


# Function to check if two lines
# are parallel or not
def parallel(a1, b1, c1, a2, b2, c2):

    # If slopes are equal
    # then ((-(a1 / b1)) == (-(a2 / b2)))
    # which is a1*b2 = a2*b1
    if a1*b2==a2*b1:
        print("Yes");
    else:
        print("No");

# Driver Code
if __name__ == '__main__':
    a1 = -2; b1 = 4; c1 = 5;
    a2 = -6; b2 = 12; c2 = 6;

    # Function Call
    parallel(a1, b1, c1, a2, b2, c2);

# This code is contributed by 29AjayKumar

C#

// C# program to implement
// the above approach
using System;
class GFG
{

// Function to check if two lines
// are parallel or not
static void parallel(float a1, float b1,
              float c1, float a2,
              float b2, float c2)
{

    // If slopes are equal
    // then (-(a1 / b1)) == (-(a2 / b2))
    // which is a1*b2 = a2*b1
    if  (a1*b2 == a2*b1)
    {
        Console.Write("Yes");
    }
    else
    {
         Console.Write("No");
    }
}

// Driver Code
public static void Main()
{
    float a1 = -2, b1 = 4, c1 = 5;
    float a2 = -6, b2 = 12, c2 = 6;

    // Function Call
    parallel(a1, b1, c1, a2, b2, c2);
}
}

// This code is contributed by susmitakundugoaldanga.

Javascript

<script>
// javascript program of the above approach

// Function to check if two lines
// are parallel or not
function parallel(a1, b1,
              c1, a2,
              b2, c2)
{

    // If slopes are equal
    // then (-(a1 / b1)) == (-(a2 / b2))
    // which is a1*b2==a2*b1
    if (a1*b2==a2*b1)
    {
        document.write("Yes");
    }
    else
    {
         document.write("No");
    }
}

    // Driver Code

    let a1 = -2, b1 = 4, c1 = 5;
    let a2 = -6, b2 = 12, c2 = 6;

    // Function Call
    parallel(a1, b1, c1, a2, b2, c2);

</script>

Output

Yes

Time Complexity: O(1)
Auxiliary Space: O(1)