Check whether two numbers are in golden ratio
Last Updated :
11 Jul, 2022
Given two numbers A and B, the task is to check that A and B are in the golden ratio.
Golden Ratio: Two numbers are said to be in the golden ratio if their ratio is the same as the ratio of the sum of the two numbers to the larger number. Here a > b > 0, Below is the geometric representation of the Golden ratio:
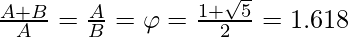

Examples:
Input: A = 1, B = 0.618
Output: Yes
Explanation:
These two numbers together forms Golden ratio
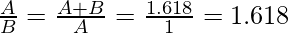
Input: A = 61.77, B = 38.22
Output Yes
Explanation:
These two numbers together forms Golden ratio
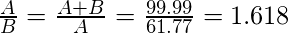
Approach: The idea is to find two ratios and check that this ratio is equal to the Golden ratio. That is 1.618.
// Here A denotes the larger number
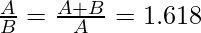
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool checkGoldenRatio(float a,
float b)
{
if(a <= b)
{
float temp = a;
a = b;
b = temp;
}
std::stringstream ratio1;
ratio1 << std :: fixed <<
std :: setprecision(3) <<
(a / b);
std::stringstream ratio2;
ratio2 << std :: fixed <<
std :: setprecision(3) <<
(a + b) / a;
if((ratio1.str() == ratio2.str()) &&
ratio1.str() == "1.618")
{
cout << "Yes" << endl;
return true;
}
else
{
cout << "No" << endl;
return false;
}
}
int main()
{
float a = 0.618;
float b = 1;
checkGoldenRatio(a, b);
return 0;
}
|
Java
class GFG{
public static Boolean checkGoldenRatio(float a,
float b)
{
if (a <= b)
{
float temp = a;
a = b;
b = temp;
}
String ratio1 = String.format("%.3f", a / b);
String ratio2 = String.format("%.3f", (a + b) / a);
if (ratio1.equals(ratio2) &&
ratio1.equals("1.618"))
{
System.out.println("Yes");
return true;
}
else
{
System.out.println("No");
return false;
}
}
public static void main(String []args)
{
float a = (float)0.618;
float b = 1;
checkGoldenRatio(a, b);
}
}
|
Python3
def checkGoldenRatio(a, b):
a, b = max(a, b), min(a, b)
ratio1 = round(a/b, 3)
ratio2 = round((a+b)/a, 3)
if ratio1 == ratio2 and\
ratio1 == 1.618:
print("Yes")
return True
else:
print("No")
return False
if __name__ == "__main__":
a = 0.618
b = 1
checkGoldenRatio(a, b)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static bool checkGoldenRatio(float a,
float b)
{
if(a <= b)
{
float temp = a;
a = b;
b = temp;
}
string ratio1 = String.Format("{0:0.000}", a / b);
string ratio2 = String.Format("{0:0.000}", (a + b) / a);
if(ratio1 == ratio2 && ratio1 == "1.618")
{
Console.WriteLine("Yes");
return true;
}
else
{
Console.WriteLine("No");
return false;
}
}
static void Main() {
float a = (float)0.618;
float b = 1;
checkGoldenRatio(a, b);
}
}
|
Javascript
<script>
function checkGoldenRatio(a, b)
{
if (a <= b)
{
let temp = a;
a = b;
b = temp;
}
let ratio1 = (a / b).toFixed(3);
let ratio2 = ((a + b) / a).toFixed(3);
if ((ratio1 == ratio2) &&
ratio1 == "1.618")
{
document.write("Yes");
return true;
}
else
{
document.write("No");
return false;
}
}
let a = 0.618;
let b = 1;
checkGoldenRatio(a, b);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
References: https://en.wikipedia.org/wiki/Golden_ratio
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...