Check whether the given number is Wagstaff prime or not
Last Updated :
26 Apr, 2021
Given a positive integer n, the task is to check if it is a Wagstaff prime or not. Print ‘YES’ if the given number is Wagstaff prime otherwise print ‘NO’.
Wagstaff prime: In mathematics, Wagstaff prime is a prime number ‘n’ of the form 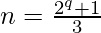
where ‘q’ is an odd prime.
First, few Wagstaff prime numbers are:
3, 11, 43, 683, 2731, 43691, 174763, 2796203……….
Examples:
Input: 43
Output: Yes
43 can be expressed as - (27 + 1 )/ 3
Input: 31
Output: No
31 can not be expressed in above mentioned form.
Approach:
- Check first if the given number is a prime number or not. To check for a number to be prime, refer this.
- Then check if it can be expressed in the form of (n * 3 – 1) and should be a power of 2. To check for a number to be a power of 2, refer this.
- If both conditions are true, then the number is a Wagstaff prime number. Hence, print “YES”. Otherwise, print “NO”
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
bool isPowerOfTwo(int n)
{
return (n && !(n & (n - 1)));
}
int main()
{
int n = 43;
if (isPrime(n) && (isPowerOfTwo(n * 3 - 1))) {
cout << "YES\n";
}
else {
cout << "NO\n";
}
return 0;
}
|
Java
class GFG {
static boolean isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
static boolean isPowerOfTwo(int n)
{
return n != 0 && ((n & (n - 1)) == 0);
}
public static void main(String[] args)
{
int n = 43;
if (isPrime(n) && (isPowerOfTwo(n * 3 - 1))) {
System.out.println("YES");
}
else {
System.out.println("NO");
}
}
}
|
Python3
def isPrime(n) :
if (n <= 1) :
return False
if (n <= 3) :
return True
if (n % 2 == 0 or n % 3 == 0) :
return False
i = 5
while(i * i <= n) :
if (n % i == 0 or n % (i + 2) == 0) :
return False
i = i + 6
return True
def isPowerOfTwo(n):
return (n and (not(n & (n - 1))))
n = 43
if(isPrime(n) and isPowerOfTwo(n * 3-1)):
print("YES")
else:
print("NO")
|
C#
using System;
class GFG
{
static bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5;
i * i <= n; i = i + 6)
{
if (n % i == 0 ||
n % (i + 2) == 0)
{
return false;
}
}
return true;
}
static bool isPowerOfTwo(int n)
{
return n != 0 && ((n & (n - 1)) == 0);
}
public static void Main()
{
int n = 43;
if (isPrime(n) &&
(isPowerOfTwo(n * 3 - 1)))
{
Console.WriteLine("YES");
}
else
{
Console.WriteLine("NO");
}
}
}
|
PHP
<?php
function isPrime($n)
{
if ($n <= 1)
return false;
if ($n <= 3)
return true;
if ($n % 2 == 0 or $n % 3 == 0)
return false;
for ($i = 5;
$i * $i <= $n; $i = $i + 6)
{
if ($n % $i == 0 or
$n % ($i + 2) == 0)
{
return false;
}
}
return true;
}
function isPowerOfTwo($n)
{
return ($n && !($n & ($n - 1)));
}
$n = 43;
if (isPrime($n) &&
(isPowerOfTwo($n * 3 - 1)))
{
echo "YES";
}
else
{
echo"NO";
}
?>
|
Javascript
<script>
function isPrime( n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (var i = 5; i * i <= n; i = i + 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
function isPowerOfTwo(n)
{
return (n != 0 )&& ((n & (n - 1)) == 0);
}
var n = 43;
if (isPrime(n) && (isPowerOfTwo(n * 3 - 1))) {
document.write("YES");
}
else {
document.write("NO");
}
</script>
|
Time Complexity: O(n1/2)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...