Check whether right angled triangle is valid or not for large sides
Last Updated :
09 Aug, 2022
Given three integers a, b and c as triplets. Check if it is possible to make right angled triangle or not. Print Yes if possible, else No. 10-18 <= a, b, c <= 1018
Examples:
Input: 3 4 5
Output: Yes
Explanation:
Since 3*3 + 4*4 = 5*5
Hence print "Yes"
Input: 8 5 13
Since 8 + 5 < 13 which violates the property of
triangle. Hence print "No"
For a right angled triangle to be valid it must satisfies the following criteria:-
a, b and c should be greater than 0.
Sum of any two sides of triangle must be greater than the third side.
Pythagorean Theorem i.e., a2 + b2 = c2.
First two conditions can be easily checked but for third condition we have to take care of overflow. Since a, b and c can be large so we can’t compare them directly unless we use python or BigInteger library in Java. For languages like C and C++, we have to reduce the expression in fraction form.
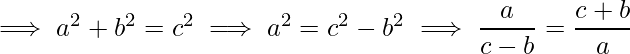
Before comparing the fraction we need convert them in simplified form by dividing the numerator and denominator by gcd of both of them. Now compare both numerator and denominator of both the fractions of LHS and RHS such that if both would become same then it signifies the valid right angled triangle otherwise not.
C++
Java
Python3
C#
Javascript
Output:
Yes
No
Yes
Time complexity: O(log(M)) where M is the Maximum value among a, b and c.
Auxiliary space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...