Check whether one root of the Quadratic Equation is twice of other or not
Last Updated :
23 Jun, 2021
Given three numbers A, B, C which represents the coefficients(constants) of a quadratic equation 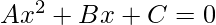 , the task is to check whether one root of the equation represented by these constants is twice of other or not.
, the task is to check whether one root of the equation represented by these constants is twice of other or not.
Examples:
Input: A = 1, B = -3, C = 2
Output: Yes
Explanation:
The given quadratic equation is 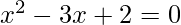
Its roots are (1, 2). 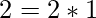
Input: A = 1, B = -5, C = 6
Output: No
Explanation:
The given quadratic equation is 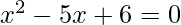
Its roots are (2, 3). 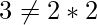 or
or 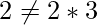
Approach: The idea is to use the concept of quadratic roots to solve the problem. We can formulate the condition required to check whether one root is twice of the other or not by:
- The sum of roots =
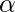 +
+  = 3
= 3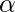 . This value is equal to:
. This value is equal to:
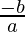
- Similarly, the product of the roots =
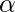 *
*  = 2
= 2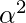 . This value is equal to:
. This value is equal to:
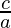
- We can solve the above two equations
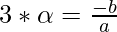 and
and 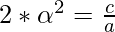 to get the condition:
to get the condition:
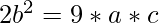
- Therefore, inorder for the first assumption of the roots to hold true, the above condition needs to hold true. Hence, we simply check if the above condition is true or not for the given coefficients.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void checkSolution(int a, int b, int c)
{
if (2 * b * b == 9 * a * c)
cout << "Yes";
else
cout << "No";
}
int main()
{
int a = 1, b = 3, c = 2;
checkSolution(a, b, c);
return 0;
}
|
Java
class GFG{
static void checkSolution(int a, int b, int c)
{
if (2 * b * b == 9 * a * c)
System.out.print("Yes");
else
System.out.print("No");
}
public static void main(String[] args)
{
int a = 1, b = 3, c = 2;
checkSolution(a, b, c);
}
}
|
Python3
def checkSolution(a, b, c):
if (2 * b * b == 9 * a * c):
print("Yes");
else:
print("No");
a = 1; b = 3; c = 2;
checkSolution(a, b, c);
|
C#
using System;
class GFG{
static void checkSolution(int a, int b, int c)
{
if (2 * b * b == 9 * a * c)
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
public static void Main()
{
int a = 1, b = 3, c = 2;
checkSolution(a, b, c);
}
}
|
Javascript
<script>
function checkSolution(a, b, c)
{
if (2 * b * b == 9 * a * c)
document.write("Yes");
else
document.write("No");
}
let a = 1, b = 3, c = 2;
checkSolution(a, b, c);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...