Check whether a number is Good prime or not
Last Updated :
08 May, 2023
Given a positive integer N, the task is to check whether the given number is good prime or not. If the given number is good prime print ‘YES’ Otherwise Print ‘NO’.
Good Prime: In Mathematics, a good prime is a prime number whose square is greater than the product of any two primes at the same number of positions before and after it in the sequence of primes. In other word, A prime Pn is said to be good prime if it 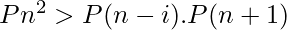 for every 1 <= i < n.
for every 1 <= i < n.
The first few good primes are: 5, 11, 17, 29, 37, 41, 53, 59, 67, 71, 97, 101, 127, 149, 179, 191, 223, ….
Examples:
Input: N = 5
Output: YES
Explanation: 5 is a good prime number
since 5^2 = 25 is greater than 3.7 = 21
and 2.11 = 22.
Input: N = 20
Output: NO
Approach:
1. Get the number N.
2. Initialise prev_prime = N-1 and next_prime = N+1
3. Iterate the loop while prev_prime is greater than or equal to 2. And check for both next_prime and prev_prime are prime of not using prime number.
4. If both are not prime, then repeat step 2 and 3.
5. If both next_prime and prev_prime are prime, then check N^2 > next_prime . prev_prime or not.
- If Not then number is not good prime and stop the execution and return NO.
- If Yes then repeat the step 2, 3, 4 and 5.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
bool isPrime (int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(int i = 5; i * i <= n; i += 6)
{
if (n % i == 0 || n % (i + 2) == 0)
return false;
}
return true;
}
bool isGoodprime (int n)
{
if (n < 5)
return false;
int prev_prime = n - 1;
int next_prime = n + 1;
while (prev_prime >= 2)
{
while (!isPrime(prev_prime))
{
prev_prime--;
}
while (!isPrime(next_prime))
{
next_prime++;
}
if ((prev_prime * next_prime) >= n * n)
return false;
prev_prime -= 1;
next_prime += 1;
}
return true;
}
int main()
{
int n = 11;
if (isGoodprime(n))
cout << "YES";
else
cout << "NO";
return 0;
}
|
Java
class GFG{
static boolean isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(int i = 5; i * i <= n; i = i + 6)
{
if (n % i == 0 || n % (i + 2) == 0)
{
return false;
}
}
return true;
}
static boolean isGoodrprime(int n)
{
if (n < 5)
return false;
int prev_prime = n - 1;
int next_prime = n + 1;
while (prev_prime >= 2)
{
while (!isPrime(prev_prime))
{
prev_prime--;
}
while (!isPrime(next_prime))
{
next_prime++;
}
if ((prev_prime * next_prime) >= n * n)
return false;
prev_prime -= 1;
next_prime += 1;
}
return true;
}
public static void main(String []args)
{
int n = 11;
if (isGoodrprime(n))
System.out.println("YES");
else
System.out.println("NO");
}
}
|
Python3
def isPrime(n):
if (n <= 1):
return False
if (n <= 3):
return True
if (n % 2 == 0 or n % 3 == 0):
return False
i = 5
while (i * i <= n):
if (n % i == 0 or n % (i + 2) == 0):
return False
i = i + 6
return True
def isGoodrPrime(n):
global next_prime, prev_prime
if(n < 5):
return False
prev_prime = n - 1
next_prime = n + 1
while(prev_prime >= 2):
while (not isPrime(prev_prime)):
prev_prime -= 1
while(not isPrime(next_prime)):
next_prime += 1
if((prev_prime * next_prime) >= n * n):
return False
prev_prime -= 1
next_prime += 1
return True
if __name__ == '__main__':
n = 11
if(isGoodrPrime(n)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG {
static bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
static bool isGoodrprime(int n)
{
if (n < 5)
return false;
int prev_prime = n - 1;
int next_prime = n + 1;
while (prev_prime >= 2) {
while (!isPrime(prev_prime)) {
prev_prime--;
}
while (!isPrime(next_prime)) {
next_prime++;
}
if ((prev_prime * next_prime)
>= n * n)
return false;
prev_prime -= 1;
next_prime += 1;
}
return true;
}
public static void Main()
{
int n = 11;
if (isGoodrprime(n))
Console.WriteLine("YES");
else
Console.WriteLine("NO");
}
}
|
Javascript
<script>
function isPrime (n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(let i = 5; i * i <= n; i += 6)
{
if (n % i == 0 || n % (i + 2) == 0)
return false;
}
return true;
}
function isGoodprime (n)
{
if (n < 5)
return false;
let prev_prime = n - 1;
let next_prime = n + 1;
while (prev_prime >= 2)
{
while (!isPrime(prev_prime))
{
prev_prime--;
}
while (!isPrime(next_prime))
{
next_prime++;
}
if ((prev_prime * next_prime) >= n * n)
return false;
prev_prime -= 1;
next_prime += 1;
}
return true;
}
let n = 11;
if (isGoodprime(n))
document.write("YES");
else
document.write("NO");
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...