Check if two nodes are on same path in a tree
Last Updated :
03 Feb, 2021
Given a tree (not necessarily a binary tree) and a number of queries such that every query takes two nodes of the tree as parameters. For every query pair, find if two nodes are on the same path from the root to the bottom.
For example, consider the below tree, if given queries are (1, 5), (1, 6), and (2, 6), then answers should be true, true, and false respectively.
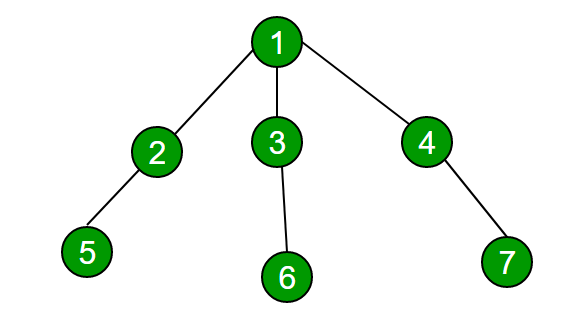
Note that 1 and 5 lie on the same root to leaf path, so do 1 and 6, but 2 and 6 are not on the same root to leaf path.
It is obvious that the Depth First Search technique is to be used to solve the above problem, the main problem is how to respond to multiple queries fast. Here our graph is a tree which may have any number of children. Now DFS in a tree, if started from root node, proceeds in a depth search manner i.e. Suppose root has three children and those children have only one child with them so if DFS is started then it first visits the first child of root node then will go deep to the child of that node. The situation with a small tree can be shown as follows:
The order of visiting the nodes will be – 1 2 5 3 6 4 7 .
Thus, other children nodes are visited later until completely one child is successfully visited till depth. To simplify this if we assume that we have a watch in our hand, and we start walking from the root in DFS manner.
Intime – When we visit the node for the first time
Outtime- If we again visit the node later but there are no children unvisited we call it outtime,
Note: Any node in its sub-tree will always have intime < its children (or children of children) because it is always visited first before children (due to DFS) and will have outtime > all nodes in its sub-tree because before noting the outtime it waits for all of its children to be marked visited.
For any two nodes u, v if they are in the same path then,
Intime[v] < Intime[u] and Outtime[v] > Outtime[u]
OR
Intime[u] < Intime[v] and Outtime[u ]> Outtime[v]
- If a given pair of nodes follows any of the two conditions, then they are on the same root to the leaf path.
- Else not on the same path (If two nodes are on different paths it means that no one is in the subtree of each other).
Pseudo Code
We use a global variable time which will be incremented as dfs for a node begins and will also be incremented after
DFS(v)
increment timer
Intime[v] = timer
mark v as visited
for all u that are children of v
DFS(u)
increment timer
Outtime[v] = timer
end
Time Complexity – O(n) for preprocessing and O(1) per query.
Implementation:
Below is the implementation of the above pseudo-code.
C++
#include<bits/stdc++.h>
using namespace std;
const int MAX = 100001;
bool visit[MAX] = {0};
int intime[MAX];
int outtime[MAX];
int timer = 0;
void dfs(vector<int> graph[], int v)
{
visit[v] = true;
++timer;
intime[v] = timer;
vector<int>::iterator it = graph[v].begin();
while (it != graph[v].end())
{
if (visit[*it]==false)
dfs(graph, *it);
it++;
}
++timer;
outtime[v] = timer;
}
bool query(int u, int v)
{
return ( (intime[u]<intime[v] && outtime[u]>outtime[v]) ||
(intime[v]<intime[u] && outtime[v]>outtime[u]) );
}
int main()
{
int n = 9;
vector<int> graph[n+1];
graph[1].push_back(2);
graph[1].push_back(3);
graph[3].push_back(6);
graph[2].push_back(4);
graph[2].push_back(5);
graph[5].push_back(7);
graph[5].push_back(8);
graph[5].push_back(9);
dfs(graph, 1);
query(1, 5)? cout << "Yes\n" : cout << "No\n";
query(2, 9)? cout << "Yes\n" : cout << "No\n";
query(2, 6)? cout << "Yes\n" : cout << "No\n";
return 0;
}
|
Java
import java.util.*;
class GFG{
static int MAX = 100001;
static boolean []visit = new boolean[MAX];
static int []intime = new int[MAX];
static int []outtime = new int[MAX];
static int timer = 0;
static void dfs(Vector<Integer> graph[], int v)
{
visit[v] = true;
++timer;
intime[v] = timer;
for(int it : graph[v])
{
if (visit[it] == false)
dfs(graph, it);
it++;
}
++timer;
outtime[v] = timer;
}
static boolean query(int u, int v)
{
return ((intime[u] < intime[v] &&
outtime[u] > outtime[v]) ||
(intime[v] < intime[u] &&
outtime[v] > outtime[u]));
}
public static void main(String[] args)
{
int n = 9;
@SuppressWarnings("unchecked")
Vector<Integer> []graph = new Vector[n + 1];
for(int i = 0; i < graph.length; i++)
graph[i] = new Vector<Integer>();
graph[1].add(2);
graph[1].add(3);
graph[3].add(6);
graph[2].add(4);
graph[2].add(5);
graph[5].add(7);
graph[5].add(8);
graph[5].add(9);
dfs(graph, 1);
if (query(1, 5))
System.out.print("Yes\n" );
else
System.out.print("No\n");
if (query(2, 9))
System.out.print("Yes\n");
else
System.out.print("No\n");
if (query(2, 6))
System.out.print("Yes\n" );
else
System.out.print("No\n");
}
}
|
Python3
def dfs(graph, v):
global intime, outtime, visit, MAX, timer
visit.add(v)
timer += 1
intime[v] = timer
it = 0
while it < len(graph[v]):
if (graph[v][it] not in visit):
dfs(graph, graph[v][it])
it += 1
timer += 1
outtime[v] = timer
def query(u, v):
global intime, outtime, visit, MAX, timer
return ((intime[u] < intime[v] and
outtime[u] > outtime[v]) or
(intime[v] < intime[u] and
outtime[v] > outtime[u]) )
MAX = 100001
visit =set()
intime = [0] * MAX
outtime = [0] * MAX
timer = 0
n = 9
graph = [[] for i in range(n+1)]
graph[1].append(2)
graph[1].append(3)
graph[3].append(6)
graph[2].append(4)
graph[2].append(5)
graph[5].append(7)
graph[5].append(8)
graph[5].append(9)
dfs(graph, 1)
print("Yes") if query(1, 5) else print("No")
print("Yes") if query(2, 9) else print("No")
print("Yes") if query(2, 6) else print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int MAX = 100001;
static bool []visit =
new bool[MAX];
static int []intime =
new int[MAX];
static int []outtime =
new int[MAX];
static int timer = 0;
static void dfs(List<int> []graph,
int v)
{
visit[v] = true;
++timer;
intime[v] = timer;
foreach(int it in graph[v])
{
if (visit[it] == false)
dfs(graph, it);
}
++timer;
outtime[v] = timer;
}
static bool query(int u,
int v)
{
return ((intime[u] < intime[v] &&
outtime[u] > outtime[v]) ||
(intime[v] < intime[u] &&
outtime[v] > outtime[u]));
}
public static void Main(String[] args)
{
int n = 9;
List<int> []graph =
new List<int>[n + 1];
for(int i = 0;
i < graph.Length; i++)
graph[i] = new List<int>();
graph[1].Add(2);
graph[1].Add(3);
graph[3].Add(6);
graph[2].Add(4);
graph[2].Add(5);
graph[5].Add(7);
graph[5].Add(8);
graph[5].Add(9);
dfs(graph, 1);
if (query(1, 5))
Console.Write("Yes\n" );
else
Console.Write("No\n");
if (query(2, 9))
Console.Write("Yes\n");
else
Console.Write("No\n");
if (query(2, 6))
Console.Write("Yes\n" );
else
Console.Write("No\n");
}
}
|
Illustration:
From the diagram below to understand more, we can have some examples. DFS algorithm as modified above will result in the following intime and outtime for the vertex of the tree as labeled there. Now we will consider all the cases.
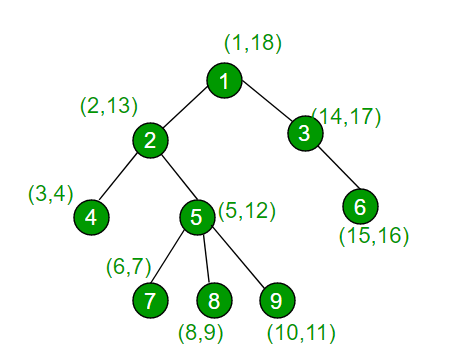
Case 1: Nodes 2 and 4: Node 2 has intime less than node 4 but since 4 is in its sub tree so it will have a greater exit time than 4 . Thus, condition is valid and both are on the same path.
Case 2: Nodes 7 and 6: Node 7 has intime less than node 6 but since both nodes are not in each other’s sub tree so their exit time does not follow the required condition.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...