Check if roots of a Quadratic Equation are numerically equal but opposite in sign or not
Last Updated :
23 Aug, 2021
Given the coefficients (constants) of a quadratic equation 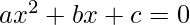 , i.e. a, b, and c; the task is to check whether roots of the equation represented by these constants are numerically equal but opposite in sign or not.
, i.e. a, b, and c; the task is to check whether roots of the equation represented by these constants are numerically equal but opposite in sign or not.
Examples:
Input: a = 2, b = 0, c = -1
Output: Yes
Explanation:
The given quadratic equation is 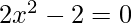
Its roots are (1, -1) which are numerically equal but opposite in sign
Input: a = 1, b = -5, c = 6
Output: No
Explanation:
The given quadratic equation is 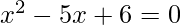
Its roots are (2, 3) which are not numerically equal and opposite in sign
Approach:
To check whether roots are numerically equal but opposite in sign or not:
Quadratic Equation: 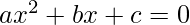
Let the roots be 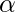 and
and 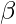
Sum of roots = 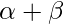 =
= 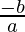
Since roots are opposite in sign only, therefore 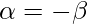
Therefore,
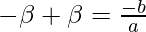
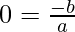
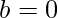 , i.e, coefficient of x is 0.
, i.e, coefficient of x is 0.
Hence we have to only check if b is 0 or not, for the roots to be numerically equal but opposite in sign.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void checkSolution(int a, int b, int c)
{
if (b == 0)
cout << "Yes";
else
cout << "No";
}
int main()
{
int a = 2, b = 0, c = 2;
checkSolution(a, b, c);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void checkSolution(int a, int b, int c)
{
if (b == 0)
System.out.print("Yes");
else
System.out.print("No");
}
public static void main(String args[])
{
int a = 2, b = 0, c = 2;
checkSolution(a, b, c);
}
}
|
Python3
def checkSolution(a, b, c):
if b == 0:
print("Yes")
else:
print("No")
a = 2
b = 0
c = 2
checkSolution(a, b, c)
|
C#
using System;
class GFG{
static void checkSolution(int a, int b, int c)
{
if (b == 0)
Console.Write("Yes");
else
Console.Write("No");
}
public static void Main()
{
int a = 2, b = 0, c = 2;
checkSolution(a, b, c);
}
}
|
Javascript
<script>
function checkSolution(a, b, c)
{
if (b == 0)
document.write("Yes");
else
document.write("No");
}
a = 2, b = 0, c = 2;
checkSolution(a, b, c);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...