Check if N is a Balanced Prime number or not
Last Updated :
18 Mar, 2021
Given a positive integer N, the task is to check if N is a Balanced Prime number or not.
In number theory, a Balanced Prime is a prime number with equal-sized prime gaps above and below it, so that it is equal to the arithmetic mean of the nearest primes above and below. Or to put it algebraically, given a prime number p<sub>n</sub>, where n is its index in the ordered set of prime numbers,
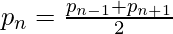
First few balanced prime are 5, 53, 157, 173……
Examples:
Input: N = 5
Output: Yes
5 is 3rd prime number, the arithmetic mean of 2nd and 4th prime number i.e. 3 and 7 is 5.
so 5 is a Balanced prime.
Input: N = 11
Output: No
Approach:
- If N is not a prime number or it is the first prime number i.e. 2 then print No.
- Else find the primes closest to N (one on the left and one on the right) and store their arithmetic mean in mean.
- If N == mean then print Yes.
- Else print No.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
bool isBalancedPrime(int n)
{
if (!isPrime(n) || n == 2)
return false;
int previous_prime = n - 1;
int next_prime = n + 1;
while (!isPrime(next_prime))
next_prime++;
while (!isPrime(previous_prime))
previous_prime--;
int mean = (previous_prime +
next_prime) / 2;
if (n == mean)
return true;
else
return false;
}
int main()
{
int n = 53;
if (isBalancedPrime(n))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
class GFG{
static boolean isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(int i = 5; i * i <= n; i += 6)
if (n % i == 0 ||
n % (i + 2) == 0)
return false;
return true;
}
static boolean isBalancedPrime(int n)
{
if (!isPrime(n) || n == 2)
return false;
int previous_prime = n - 1;
int next_prime = n + 1;
while (!isPrime(next_prime))
next_prime++;
while (!isPrime(previous_prime))
previous_prime--;
int mean = (previous_prime +
next_prime) / 2;
if (n == mean)
return true;
else
return false;
}
public static void main(String[] args)
{
int n = 53;
if (isBalancedPrime(n))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def isPrime(n):
if n <= 1:
return False
if n <= 3:
return True
if n % 2 == 0 or n % 3 == 0:
return False
i = 5
while i * i <= n:
if (n % i == 0 or
n % (i + 2) == 0):
return False
i += 6
return True
def isBalancedPrime(n):
if not isPrime(n) or n == 2:
return False
previous_prime = n - 1
next_prime = n + 1
while not isPrime(next_prime):
next_prime += 1
while not isPrime(previous_prime):
previous_prime -= 1
mean = (previous_prime +
next_prime) / 2
if n == mean:
return True
else:
return False
n = 53
if isBalancedPrime(n):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG {
static bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
static bool isBalancedPrime(int n)
{
if (!isPrime(n) || n == 2)
return false;
int previous_prime = n - 1;
int next_prime = n + 1;
while (!isPrime(next_prime))
next_prime++;
while (!isPrime(previous_prime))
previous_prime--;
int mean = (previous_prime
+ next_prime)
/ 2;
if (n == mean)
return true;
else
return false;
}
public static void Main()
{
int n = 53;
if (isBalancedPrime(n))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
function isPrime(n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for(let i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
function isBalancedPrime(n)
{
if (!isPrime(n) || n == 2)
return false;
let previous_prime = n - 1;
let next_prime = n + 1;
while (!isPrime(next_prime))
next_prime++;
while (!isPrime(previous_prime))
previous_prime--;
let mean = (previous_prime +
next_prime) / 2;
if (n == mean)
return true;
else
return false;
}
let n = 53;
if (isBalancedPrime(n))
document.write("Yes");
else
document.write("No");
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...