Check if N can be divided into K consecutive elements with a sum equal to N
Last Updated :
25 Mar, 2021
Given an integer N, our task is to check if N can be divided into K consecutive elements with a sum equal to N. Print -1 if it is not possible to divide in this manner, otherwise print the value K.
Examples:
Input: N = 12
Output: 3
Explanation:
The integer N = 12 can be divided into 3 consecutive elements {3, 4, 5} where 3 + 4 + 5 = 12.
Input: N = 8
Output: -1
Explanation:
No such division of integer 8 is possible.
Approach: To solve the problem mentioned above let us divide the integer N into i consecutive numbers. The terms of the sequence will look like (d+1), (d+2), (d+3)…..(d+i) where d is the common difference present in each of the integers and the sum of this sequence should be equal to N.
So, the sum of these number can also be expressed as:
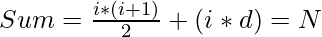
As the sum = i * (i + 1) / 2 grows quadratically, we have, N – sum = i * d. Hence, for a solution to exist, the number of integers should evenly divide the quantity N – sum. Below are the steps:
- Iterate from index(say i) from 2.
- Find the sum of first i numbers(say sum).
- For any iteration if (N – sum) is divisible by i then print that value of i.
- For any iteration if N exceeds the sum then print “-1”.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void canBreakN(long long n)
{
for (long long i = 2;; i++) {
long long m = i * (i + 1) / 2;
if (m > n)
break;
long long k = n - m;
if (k % i)
continue;
cout << i << endl;
return;
}
cout << "-1";
}
int main()
{
long long N = 12;
canBreakN(N);
return 0;
}
|
Java
class GFG{
public static void canBreakN(long n)
{
for(long i = 2;; i++)
{
long m = i * (i + 1) / 2;
if (m > n)
break;
long k = n - m;
if (k % i != 0)
continue;
System.out.println(i);
return;
}
System.out.println("-1");
}
public static void main(String[] args)
{
long N = 12;
canBreakN(N);
}
}
|
Python3
def canBreakN(n):
for i in range(2, n):
m = i * (i + 1) // 2
if (m > n):
break
k = n - m
if (k % i):
continue
print(i)
return
print("-1")
N = 12
canBreakN(N)
|
C#
using System;
class GFG{
public static void canBreakN(long n)
{
for(long i = 2;; i++)
{
long m = i * (i + 1) / 2;
if (m > n)
break;
long k = n - m;
if (k % i != 0)
continue;
Console.Write(i);
return;
}
Console.Write("-1");
}
public static void Main(string[] args)
{
long N = 12;
canBreakN(N);
}
}
|
Javascript
<script>
function canBreakN(n)
{
for(let i = 2;; i++)
{
let m = parseInt(i * (i + 1) / 2, 10);
if (m > n)
break;
let k = n - m;
if (k % i != 0)
continue;
document.write(i);
return;
}
document.write("-1");
}
let N = 12;
canBreakN(N);
</script>
|
Time Complexity: O(K), where K is the number of element whose sum is K.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...