Check if elements of an array can be arranged in a Circle with consecutive difference as 1

Given an array of 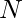N numbers. The task is to check if it is possible to arrange all the numbers in a circle so that any two neighboring numbers differ exactly by 1. Print “YES” if it is possible to get such arrangement and “NO” otherwise.

Examples:

Input: arr[] = {1, 2, 3, 2}
Output: YES
The circle formed is:
         1
     2       2
         3   

Input: arr[] = {3, 5, 8, 4, 7, 6, 4, 7}
Output: NO

Below is the step by step algorithm to solve this problem:



  1. First insert all the elements in a multiset.
  2. Remove the first element of the set and store it in a curr variable.
  3. Traverse until the size of multiset reduced to 0.
    • Remove elements that are 1 greater or 1 smaller than the curr value.
    • If there is a value with difference more than 1 then “no circle possible”.
  4. Check if it’s initial and final values of curr varaible are same, print “YES” if it is, otherwise print “NO”.

Below is the implementaion of above approach:

filter_none

edit
close

play_arrow

link
brightness_4
code

// C++ program to check if elements of array
// can be arranged in Circle with consecutive
// difference as 1
  
#include <bits/stdc++.h>
using namespace std;
  
// Function to check if elements of array can
// be arranged in Circle with consecutive
// difference as 1
int circlePossible(int arr[], int n)
{
    multiset<int> s;
  
    // Initialize the multiset with array
    // elements
    for (int i = 0; i < n; i++)
        s.insert(arr[i]);
  
    // Get a pointer to first element
    int cur = *s.begin();
  
    // Store the first element in a temp variable
    int start = cur;
  
    // Remove the first element
    s.erase(s.begin());
  
    // Traverse until multiset is non-empty
    while (s.size()) {
  
        // Elements which are 1 greater than the
        // current element, remove their first occurrence
        // and increment curr
        if (s.find(cur + 1) != s.end())
            s.erase(s.find(++cur));
  
        // Elements which are 1 less than the
        // current element, remove their first occurrence
        // and decrement curr
        else if (s.find(cur - 1) != s.end())
            s.erase(s.find(--cur));
  
        // If the set is non-empty and contains element
        // which differs by curr from more than 1
        // then circle is not possible return
        else {
            cout << "NO";
            return 0;
        }
    }
  
    // Finally, check if curr and first differs by 1
    if (abs(cur - start) == 1)
        cout << "YES";
    else
        cout << "NO";
  
    return 0;
}
  
// Driver code
int main()
{
    int arr[] = { 1, 1, 2, 2, 2, 3 };
  
    int n = sizeof(arr) / sizeof(arr[0]);
  
    circlePossible(arr, n);
  
    return 0;
}

chevron_right






                        filter_none









Output:


YES





competitive-programming-img





    

        My Personal Notes
        arrow_drop_up
    

    

        
        

            
            
        

    


Recommended Posts:
SrijaDe
Check out this Author's contributed articles.
If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please Improve this article if you find anything incorrect by clicking on  the "Improve Article" button below.