Check if any large number is divisible by 17 or not

Given a number, the task is to quickly check if the number is divisible by 17 or not. 
Example:

Input : x = 34
Output : Yes
Input : x = 47
Output : No

A solution to the problem is to extract the last digit and subtract 5 times of the last digit from the remaining number and repeat this process until a two-digit number is obtained. If the obtained two-digit number is divisible by 17, then the given number is divisible by 17.
Approach:

• Extract the last digit of the number/truncated number every time
• Subtract 5*(last digit of the previous number) from the truncated number
• Repeat the above three steps as long as necessary.

Illustration:

3978-->397-5*8=357-->35-5*7=0. 
So 3978 is divisible by 17.

Mathematical Proof : 
Let 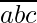be any number such that 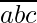=100a+10b+c . 
Now assume that 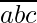is divisible by 17. Then 
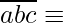0 (mod 17) 
100a+10b+c0 (mod 17) 
10(10a+b)+c0 (mod 17) 
10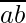+c0 (mod 17)
Now that we have separated the last digit from the number, we have to find a way to use it. 
Make the coefficient of 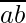1. 
In other words, we have to find an integer such that n such that 10n1 mod 17. 
It can be observed that the smallest n which satisfies this property is -5 as -501 mod 17. 
Now we can multiply the original equation 10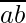+c0 (mod 17) 
by -5 and simplify it: 
-50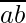-5c0 (mod 17) 
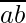-5c0 (mod 17) 
We have found out that if 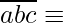0 (mod 17) then, 
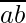-5c0 (mod 17). 
In other words, to check if a 3-digit number is divisible by 17, 
we can just remove the last digit, multiply it by 5, 
and then subtract it from the rest of the two digits. 

Program :

C++

// CPP Program to validate the above logic
#include <bits/stdc++.h>

using namespace std;

// Function to check if the
// number is divisible by 17 or not
bool isDivisible(long long int n)
{

    while (n / 100)
    {
        // Extracting the last digit
        int d = n % 10;

        // Truncating the number
        n /= 10;

        // Subtracting the five times the
        // last digit from the remaining number
        n -= d * 5;
    }

    // Return n is divisible by 17
    return (n % 17 == 0);
}

// Driver code
int main()
{
    long long int n = 19877658;
    if (isDivisible(n))
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
    return 0;
}

Java

// Java Program to validate the above logic

import java.io.*;

class GFG {


// Function to check if the
// number is divisible by 17 or not
 static boolean isDivisible(long n)
{

    while (n / 100>0)
    {
        // Extracting the last digit
        long d = n % 10;

        // Truncating the number
        n /= 10;

        // Subtracting the five times the
        // last digit from the remaining number
        n -= d * 5;
    }

    // Return n is divisible by 17
    return (n % 17 == 0);
}

// Driver code

    public static void main (String[] args) {
    long n = 19877658;
    if (isDivisible(n))
        System.out.println( "Yes");
    else
        System.out.println( "No");
    }
}
// This code is contributed by inder_verma.

Python 3

# Python 3 Program to validate
# the above logic

# Function to check if the
# number is divisible by 17 or not
def isDivisible(n) :

    while(n // 100) :

        # Extracting the last digit
        d = n % 10

        # Truncating the number
        n //= 10

        # Subtracting the five times
        # the last digit from the
        # remaining number
        n -= d * 5

    # Return n is divisible by 17
    return (n % 17 == 0)

# Driver Code
if __name__ == "__main__" :

    n = 19877658

    if isDivisible(n) :
        print("Yes")
    else :
        print("No")

# This code is contributed
# by ANKITRAI1

C#

// C# Program to validate the above logic

using System;

class GFG {


// Function to check if the
// number is divisible by 17 or not
 static bool isDivisible(long n)
{

    while (n / 100>0)
    {
        // Extracting the last digit
        long d = n % 10;

        // Truncating the number
        n /= 10;

        // Subtracting the five times the
        // last digit from the remaining number
        n -= d * 5;
    }

    // Return n is divisible by 17
    return (n % 17 == 0);
}

// Driver code

    public static void Main () {
    long n = 19877658;
    if (isDivisible(n))
        Console.Write( "Yes");
    else
        Console.Write( "No");
    }
}

Javascript

// Function to check if the
// number is divisible by 17 or not
function isDivisible(n) {
    while (Math.floor(n / 100)) {
        // Extracting the last digit
        let d = n % 10;

        // Truncating the number
        n = Math.floor(n / 10);

        // Subtracting the five times the
        // last digit from the remaining number
        n -= d * 5;
    }

    // Return n is divisible by 17
    return n % 17 == 0;
}

// Driver code
let n = 19877658;
if (isDivisible(n))
    console.log("Yes");
else
    console.log("No");

PHP

<?php
// PHP Program to validate the above logic

// Function to check if the
// number is divisible by 17 or not
function isDivisible($n)
{

    while ($n / 100 != 0)
    {
        // Extracting the last digit
        $d = (int)$n % 10;

        // Truncating the number
        $n /= 10;

        // Subtracting the five times
        // the last digit from the
        // remaining number
        $n -= $d * 5;
    }

    // Return n is divisible by 17
    return ($n % 17 == 0);
}

// Driver code
$n = 19877658;
if (isDivisible($n))
    print("Yes");
else
    print("No");

// This code is contributed by Raj
?>

Output

Yes

Time Complexity: O(log₁₀n), time required to check if number is divisible by 17
Auxiliary Space: O(1), as no extra space is required

Note that the above program may not make a lot of sense as could simply do n % 23 to check for divisibility. The idea of this program is to validate the concept. Also, this might be an efficient approach if input number is large and given as string.

Approach 2: Dynamic Programming :

We can solve this problem using dynamic programming. Let’s define dp[i][j] as a boolean value that represents whether a number is divisible by 17 when we have processed the first i digits and the remainder obtained after dividing the number formed by the first i digits by 17 is j. We can fill this table in a bottom-up manner.

• The base case is dp[0][0] = true because an empty number is divisible by 17 with a remainder of 0.
• For each digit d at position i, we have two choices:
• We can ignore the digit and keep the remainder the same: dp[i][j] = dp[i-1][j].
  We can include the digit and update the remainder: dp[i][j] = dp[i-1][(j – 5*d + 17) % 17].
• The final answer is given by dp[n][0] where n is the number of digits in the original number.

       Here’s the implementation of the above approach:

C++

#include <iostream>
#include <cstring>

const int MAXN = 10; // maximum number of digits

bool isDivisibleBy17(int n) {
    char str[MAXN];
    sprintf(str, "%d", n); // convert integer to string

    int len = strlen(str);
    bool dp[len+1][17];

    memset(dp, false, sizeof(dp)); // initialize dp table

    dp[0][0] = true; // base case

    for (int i = 1; i <= len; i++) {
        int d = str[i-1] - '0'; // current digit
        for (int j = 0; j < 17; j++) {
            dp[i][j] = dp[i-1][j]; // ignore current digit
            if (j >= 5*d) {
                dp[i][j] |= dp[i-1][(j - 5*d) % 17]; // include current digit
            } else {
                dp[i][j] |= dp[i-1][(j + 17 - 5*d) % 17]; // include current digit
            }
        }
    }

    return dp[len][0];
}

int main() {
    const int n = 19877658;
    std::cout << (isDivisibleBy17(n) ? "Yes" : "No") << std::endl;
    return 0;
}

Java

/*package whatever //do not write package name here */

import java.io.*;

public class Main {
    public static boolean isDivisibleBy17(int n)
    {
        String strN = Integer.toString(n);
        int lenN = strN.length();
        boolean[][] dp = new boolean[lenN + 1][17];
        dp[0][0] = true; // base case

        for (int i = 1; i <= lenN; i++) {
            int d = Character.getNumericValue(
                strN.charAt(i - 1)); // current digit
            for (int j = 0; j < 17; j++) {
                dp[i][j]
                    = dp[i - 1][j]; // ignore current digit
                if (j >= 5 * d) {
                    dp[i][j]
                        |= dp[i - 1][(j - 5 * d)
                                     % 17]; // include
                                            // current digit
                }
                else {
                    int index = (j + 17 - 5 * d) % 17;
                    if (index < 0) {
                        index += 17;
                    }
                    dp[i][j] |= dp[i - 1]
                                  [index]; // include current digit
                }
            }
        }

        return dp[lenN][0];
    }

    public static void main(String[] args)
    {
        int n = 19877658;
        if (isDivisibleBy17(n)) {
            System.out.println("Yes");
        }
        else {
            System.out.println("No");
        }
    }
}

Python3

def is_divisible_by_17(n):
    str_n = str(n)
    len_n = len(str_n)
    dp = [[False for _ in range(17)] for _ in range(len_n + 1)]
    dp[0][0] = True # base case

    for i in range(1, len_n + 1):
        d = int(str_n[i-1]) # current digit
        for j in range(17):
            dp[i][j] = dp[i-1][j] # ignore current digit
            if j >= 5*d:
                dp[i][j] |= dp[i-1][(j - 5*d) % 17] # include current digit
            else:
                dp[i][j] |= dp[i-1][(j + 17 - 5*d) % 17] # include current digit

    return dp[len_n][0]

n = 19877658
print("Yes" if is_divisible_by_17(n) else "No")

C#

using System;

class GFG {
    public static bool IsDivisibleBy17(int n)
    {
        string strN = n.ToString();
        int lenN = strN.Length;
        bool[,] dp = new bool[lenN + 1, 17];
        dp[0, 0] = true; // base case

        for (int i = 1; i <= lenN; i++) {
            int d = int.Parse(strN[i - 1].ToString()); // current digit
            for (int j = 0; j < 17; j++) {
                dp[i, j] = dp[i - 1, j]; // ignore current digit
                if (j >= 5 * d) {
                    dp[i, j] |= dp[i - 1, (j - 5 * d) % 17]; // include current digit
                } else {
                    int index = (j + 17 - 5 * d) % 17;
                    if (index < 0) {
                        index += 17;
                    }
                    dp[i, j] |= dp[i - 1, index]; // include current digit
                }
            }
        }

        return dp[lenN, 0];
    }

    public static void Main(string[] args)
    {
        int n = 19877658;
        if (IsDivisibleBy17(n)) {
            Console.WriteLine("Yes");
        }
        else {
            Console.WriteLine("No");
        }
    }
}

Javascript

// maximum number of digits
const MAXN = 10;

function isDivisibleBy17(n) {
    // convert integer to string
    const str = n.toString();
    const len = str.length;

    // initialize dp table
    const dp = new Array(len + 1);
    for (let i = 0; i <= len; i++) {
        dp[i] = new Array(17).fill(false);
    }

    dp[0][0] = true; // base case

    for (let i = 1; i <= len; i++) {
        const d = parseInt(str.charAt(i - 1)); // current digit
        for (let j = 0; j < 17; j++) {
            dp[i][j] = dp[i - 1][j]; // ignore current digit
            if (j >= 5 * d) {
                dp[i][j] |= dp[i - 1][(j - 5 * d) % 17]; // include current digit
            } else {
                dp[i][j] |= dp[i - 1][(j + 17 - 5 * d) % 17]; // include current digit
            }
        }
    }

    return dp[len][0];
}

const n = 19877658;
console.log(isDivisibleBy17(n) ? "Yes" : "No");

Output

Yes

Time Complexity: O(N*17), where N is the number of digits in the input integer.
Auxiliary Space: O(N*17)