Check if an integer can be expressed as a sum of two semi-primes

Given a positive integer N, check if it can be expressed as a sum of two semi-primes or not.
Semi-primes A number is said to be a semi-prime if it can be expressed as product of two primes number ( not necessarily distinct ).
Semi-primes in the range 1 -100 are: 

4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87, 91, 93, 94, 95. 

Examples:

Input : N = 30
Output: YES
Explanation: 30 can be expressed as '15 + 15' 
15 is semi-primes as 15 is a product of two primes 3 and 5.

Input : N = 45
Output : YES
Explanation: 45 can be expressed as '35 + 10'
35 and 10 are also  semi-primes as it can a be expressed 
as product of two primes:
       35 = 5 * 7
       10 = 2 * 5   

Prerequisite: 

• Semi-primes
  

A Simple Solution is to traverse from i=1 to 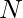and check if i and N-i are semi-primes or not. If yes, print i and n-i.
An Efficient Solution is to pre-compute semi-primes in an array up to the given range and then traverse the semi-prime array and check if n-arr[i] is semi-prime or not. As, arr[i] is already a semi-prime if n-arr[i] is also a semi-prime, then n can be expressed as sum of two semi-primes.
Below is the implementation of above approach: 

C++

// CPP Code to check if an integer
// can be expressed as sum of
// two semi-primes

#include <bits/stdc++.h>
using namespace std;
#define MAX 1000000

vector<int> arr;
bool sprime[MAX];

// Utility function to compute
// semi-primes in a range
void computeSemiPrime()
{
    memset(sprime, false, sizeof(sprime));

    for (int i = 2; i < MAX; i++) {

        int cnt = 0;
        int num = i;
        for (int j = 2; cnt < 2 && j * j <= num; ++j) {
            while (num % j == 0) {
                num /= j, ++cnt; // Increment count
                // of prime numbers
            }
        }

        // If number is greater than 1, add it to
        // the count variable as it indicates the
        // number remain is prime number

        if (num > 1)
            ++cnt;

        // if count is equal to '2' then
        // number is semi-prime

        if (cnt == 2) {

            sprime[i] = true;
            arr.push_back(i);
        }
    }
}

// Utility function to check
// if a number sum of two
// semi-primes
bool checkSemiPrime(int n)
{
    int i = 0;

    while (arr[i] <= n / 2) {

        // arr[i] is already a semi-prime
        // if n-arr[i] is also a semi-prime
        // then we a number can be expressed as
        // sum of two semi-primes

        if (sprime[n - arr[i]]) {
            return true;
        }

        i++;
    }

    return false;
}

// Driver code
int main()
{
    computeSemiPrime();

    int n = 30;
    if (checkSemiPrime(n))
        cout << "YES";
    else
        cout << "NO";

    return 0;
}

Java

// Java Code to check if an integer
// can be expressed as sum of
// two semi-primes

import java.util.*;

class GFG {

    static final int MAX = 1000000;
    static Vector<Integer> arr = new Vector<>();
    static boolean[] sprime = new boolean[MAX];

    // Utility function to compute
    // semi-primes in a range
    static void computeSemiPrime()
    {

        for (int i = 0; i < MAX; i++)
            sprime[i] = false;

        for (int i = 2; i < MAX; i++) {

            int cnt = 0;
            int num = i;
            for (int j = 2; cnt < 2 && j * j <= num; ++j) {
                while (num % j == 0) {
                    num /= j;
                    ++cnt;
                    // Increment count
                    // of prime numbers
                }
            }

            // If number is greater than 1, add it to
            // the count variable as it indicates the
            // number remain is prime number

            if (num > 1)
                ++cnt;

            // if count is equal to '2' then
            // number is semi-prime

            if (cnt == 2) {

                sprime[i] = true;
                arr.add(i);
            }
        }
    }

    // Utility function to check
    // if a number is sum of two
    // semi-primes
    static boolean checkSemiPrime(int n)
    {
        int i = 0;

        while (arr.get(i) <= n / 2) {

            // arr[i] is already a semi-prime
            // if n-arr[i] is also a semi-prime
            // then  a number can be expressed as
            // sum of two semi-primes

            if (sprime[n - arr.get(i)]) {
                return true;
            }

            i++;
        }

        return false;
    }

    // Driver code
    public static void main(String[] args)
    {
        computeSemiPrime();

        int n = 30;
        if (checkSemiPrime(n))
            System.out.println("YES");
        else
            System.out.println("NO");
    }
}

Python3

# Python3 Code to check if an integer can
# be expressed as sum of two semi-primes
MAX = 10000

arr = []
sprime = [False] * (MAX)

# Utility function to compute
# semi-primes in a range
def computeSemiPrime():

    for i in range(2, MAX):

        cnt, num, j = 0, i, 2
        while cnt < 2 and j * j <= num:
            while num % j == 0:
                num /= j

                # Increment count of prime numbers
                cnt += 1

            j += 1

        # If number is greater than 1, add it
        # to the count variable as it indicates
        # the number remain is prime number
        if num > 1:
            cnt += 1

        # if count is equal to '2' then
        # number is semi-prime
        if cnt == 2:

            sprime[i] = True
            arr.append(i)

# Utility function to check
# if a number sum of two
# semi-primes
def checkSemiPrime(n):

    i = 0
    while arr[i] <= n // 2:

        # arr[i] is already a semi-prime
        # if n-arr[i] is also a semi-prime
        # then a number can be expressed as
        # sum of two semi-primes
        if sprime[n - arr[i]] == True:
            return True

        i += 1

    return False

# Driver code
if __name__ == "__main__":

    computeSemiPrime()

    n = 30
    if checkSemiPrime(n) == True:
        print("YES")
    else:
        print("NO")

# This code is contributed by
# Rituraj Jain

C#

// C# Code to check if an integer
// can be expressed as sum of
// two semi-primes
using System.Collections.Generic;

class GFG
{

static int MAX = 1000000;
static List<int> arr = new List<int>();
static bool[] sprime = new bool[MAX];

// Utility function to compute
// semi-primes in a range
static void computeSemiPrime()
{

    for (int i = 0; i < MAX; i++)
        sprime[i] = false;

    for (int i = 2; i < MAX; i++)
    {

        int cnt = 0;
        int num = i;
        for (int j = 2; cnt < 2 && j * j <= num; ++j)
        {
            while (num % j == 0)
            {
                num /= j;
                ++cnt;

                // Increment count
                // of prime numbers
            }
        }

        // If number is greater than 1, add it to
        // the count variable as it indicates the
        // number remain is prime number
        if (num > 1)
            ++cnt;

        // if count is equal to '2' then
        // number is semi-prime

        if (cnt == 2)
        {
            sprime[i] = true;
            arr.Add(i);
        }
    }
}

// Utility function to check
// if a number is sum of two
// semi-primes
static bool checkSemiPrime(int n)
{
    int i = 0;

    while (arr[i] <= n / 2)
    {

        // arr[i] is already a semi-prime
        // if n-arr[i] is also a semi-prime
        // then a number can be expressed as
        // sum of two semi-primes

        if (sprime[n - arr[i]])
        {
            return true;
        }

        i++;
    }

    return false;
}

// Driver code
public static void Main()
{
    computeSemiPrime();

    int n = 30;
    if (checkSemiPrime(n))
        System.Console.WriteLine("YES");
    else
        System.Console.WriteLine("NO");
}
}

// This code is contributed by mits

Javascript

<script>

// Javascript Code to check if an integer
// can be expressed as sum of
// two semi-primes

var MAX = 1000000;

var arr = [];
var sprime = Array(MAX).fill(false);

// Utility function to compute
// semi-primes in a range
function computeSemiPrime()
{

    for (var i = 2; i < MAX; i++) {

        var cnt = 0;
        var num = i;
        for (var j = 2; cnt < 2 && j * j <= num; ++j) {
            while (num % j == 0) {
                num /= j, ++cnt; // Increment count
                // of prime numbers
            }
        }

        // If number is greater than 1, add it to
        // the count variable as it indicates the
        // number remain is prime number

        if (num > 1)
            ++cnt;

        // if count is equal to '2' then
        // number is semi-prime

        if (cnt == 2) {

            sprime[i] = true;
            arr.push(i);
        }
    }
}

// Utility function to check
// if a number sum of two
// semi-primes
function checkSemiPrime(n)
{
    var i = 0;

    while (arr[i] <= parseInt(n / 2)) {

        // arr[i] is already a semi-prime
        // if n-arr[i] is also a semi-prime
        // then we a number can be expressed as
        // sum of two semi-primes

        if (sprime[n - arr[i]]) {
            return true;
        }

        i++;
    }

    return false;
}

// Driver code

computeSemiPrime();
var n = 30;
if (checkSemiPrime(n))
    document.write( "YES");
else
    document.write( "NO");

// This code is contributed by itsok.
</script>

Output:

YES

Time Complexity: O(MAX*log(log(MAX))) 

Auxiliary Space: O(MAX)