Check if a triplet with given sum exists in BST
Last Updated :
12 Sep, 2022
Given a Binary Search Tree and a SUM. The task is to check if there exists any triplet(group of 3 elements) in the given BST with the given SUM.
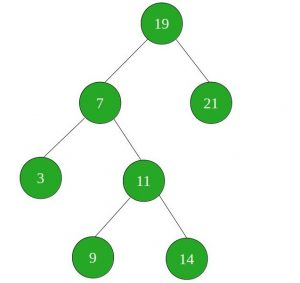
Examples:
Input : SUM = 21
Output : YES
There exists a triplet (7, 3, 11) in the
above given BST with sum 21.
Input : SUM = 101
Output : NO
It is known that elements in the inorder traversal of BST are sorted in increasing order. So, the idea is to do inorder traversal on the given BST and store the elements in a vector or array. Now the task reduces to check for a triplet with given sum in a sorted array.
Now to do this, start traversing the array and for every element A[i] check for a pair with a sum (SUM – A[i]) in the remaining sorted array.
To do this:
1) Initialize two index variables to find the candidate
elements in the sorted array.
(a) Initialize first to the leftmost index: l = 0
(b) Initialize second the rightmost index: r = ar_size-1
2) Loop while l < r.
(a) If (A[l] + A[r] == sum) then return 1
(b) Else if( A[l] + A[r] < sum ) then l++
(c) Else r--
3) If no such candidates are found in the whole array,
return 0
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
struct Node* newNode(int item)
{
Node* temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(Node* root, vector<int>& vec)
{
if (root != NULL) {
inorder(root->left, vec);
vec.push_back(root->key);
inorder(root->right, vec);
}
}
struct Node* insert(Node* node, int key)
{
if (node == NULL)
return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
bool checkForTriplet(Node* root, int sum)
{
vector<int> vec;
inorder(root, vec);
int l, r;
for (int i = 0; i < vec.size() - 2; i++) {
l = i + 1;
r = vec.size() - 1;
while (l < r) {
if (vec[i] + vec[l] + vec[r] == sum) {
return true;
}
else if (vec[i] + vec[l] + vec[r] < sum)
l++;
else
r--;
}
}
return false;
}
int main()
{
struct Node* root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
int sum = 120;
if (checkForTriplet(root, sum))
cout << "YES";
else
cout << "NO";
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class Node
{
int key;
Node left, right;
};
static Node newNode(int item)
{
Node temp = new Node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
static void inorder(Node root,
Vector<Integer> vec)
{
if (root != null)
{
inorder(root.left, vec);
vec.add(root.key);
inorder(root.right, vec);
}
}
static Node insert(Node node, int key)
{
if (node == null)
return newNode(key);
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
return node;
}
static boolean checkForTriplet(Node root, int sum)
{
Vector<Integer> vec = new Vector<Integer>();
inorder(root, vec);
int l, r;
for (int i = 0; i < vec.size() - 2; i++)
{
l = i + 1;
r = vec.size() - 1;
while (l < r)
{
if (vec.get(i) +
vec.get(l) + vec.get(r) == sum)
{
return true;
}
else if (vec.get(i) +
vec.get(l) + vec.get(r) < sum)
l++;
else
r--;
}
}
return false;
}
public static void main(String[] args)
{
Node root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
int sum = 120;
if (checkForTriplet(root, sum))
System.out.print("YES");
else
System.out.print("NO");
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.right = self.left = None
def insert(root, x):
if root is None:
root = Node(x)
else:
if root.data < x:
if root.right is None:
root.right = Node(x)
else:
insert(root.right, x)
else:
if root.left is None:
root.left = Node(x)
else:
insert(root.left, x)
def inorder(root, ior):
if root is None:
return
inorder(root.left, ior)
ior.append(root.data)
inorder(root.right, ior)
def checkForTriplet(root, sum):
vec = [0]
inorder(root, vec)
for i in range(0, len(vec) - 2, 1):
l = i + 1
r = len(vec) - 1
while(l < r):
if vec[i] + vec[l] + vec[r] == sum:
return True
elif vec[i] + vec[l] + vec[r] < sum:
l += 1
else:
r -= 1
return False
if __name__ == '__main__':
root = Node(50)
insert(root, 30)
insert(root, 20)
insert(root, 40)
insert(root, 70)
insert(root, 60)
insert(root, 80)
sum = 120
if (checkForTriplet(root, sum)):
print("YES")
else:
print("NO")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
class Node
{
public int key;
public Node left, right;
};
static Node newNode(int item)
{
Node temp = new Node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
static void inorder(Node root,
List<int> vec)
{
if (root != null)
{
inorder(root.left, vec);
vec.Add(root.key);
inorder(root.right, vec);
}
}
static Node insert(Node node, int key)
{
if (node == null)
return newNode(key);
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
return node;
}
static bool checkForTriplet(Node root, int sum)
{
List<int> vec = new List<int>();
inorder(root, vec);
int l, r;
for (int i = 0; i < vec.Count - 2; i++)
{
l = i + 1;
r = vec.Count - 1;
while (l < r)
{
if (vec[i] +
vec[l] + vec[r] == sum)
{
return true;
}
else if (vec[i] +
vec[l] + vec[r] < sum)
l++;
else
r--;
}
}
return false;
}
public static void Main(String[] args)
{
Node root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
int sum = 120;
if (checkForTriplet(root, sum))
Console.Write("YES");
else
Console.Write("NO");
}
}
|
Javascript
<script>
class Node
{
constructor()
{
this.key = 0;
this.left = null;
this.right = null;
}
};
function newNode(item)
{
var temp = new Node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
function inorder(root, vec)
{
if (root != null)
{
inorder(root.left, vec);
vec.push(root.key);
inorder(root.right, vec);
}
}
function insert(node, key)
{
if (node == null)
return newNode(key);
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
return node;
}
function checkForTriplet(root, sum)
{
var vec = [];
inorder(root, vec);
var l, r;
for (var i = 0; i < vec.length - 2; i++)
{
l = i + 1;
r = vec.length - 1;
while (l < r)
{
if (vec[i] +
vec[l] + vec[r] == sum)
{
return true;
}
else if (vec[i] +
vec[l] + vec[r] < sum)
l++;
else
r--;
}
}
return false;
}
var root = null;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
var sum = 120;
if (checkForTriplet(root, sum))
document.write("YES");
else
document.write("NO");
</script>
|
Complexity Analysis:
- Time Complexity: O(N2), as we are using nested loops, the outer loop traverses N times and the inner loop traverses N times in the worst case.
- Auxiliary Space: O(N), where N is the number of nodes in the given BST. (as we are using extra space for the tree)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...