Check if a point is inside, outside or on the parabola

Given a parabola with vertex (h, k), and 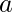, the distance between focus and vertex. The task is to determine if the point (x, y) is inside, outside or on the parabola.
Examples: 

Input: h = 100, k = 500, x = 20, y = 10, a = 4 
Output: Outside

Input: h = 0, k = 0, x = 2, y = 1, a = 4
Output: Inside

Approach: It is very simple, we have to just solve the equation for point (x, y):

(y-k)^2 = 4a(x-h)
or, (y-k)^2 – 4a(x-h) = 0

After solving, if the result comes less than 0 then the point lies within, else if it comes exact 0 then the point lies on the parabola, and if the result is greater than 0 unsatisfied the point lies outside of the parabola. 
Here we are taking a parabola whose axis of symmetry is y = k, although the approach is applicable for any parabola.
Below is the implementation of above approach: 

C++

// C++ Program to check if the point
// lies within the parabola or not
#include <bits/stdc++.h>
using namespace std;

// Function to check the point
int checkpoint(int h, int k, int x, int y, int a)
{

    // checking the equation of
    // parabola with the given point
    int p = pow((y - k), 2) - 4 * a * (x - h);

    return p;
}

// Driver code
int main()
{
    int h = 0, k = 0, x = 2, y = 1, a = 4;

    if (checkpoint(h, k, x, y, a) > 0)
        cout << "Outside" << endl;

    else if (checkpoint(h, k, x, y, a) == 0)
        cout << "On the parabola" << endl;

    else
        cout << "Inside" << endl;

    return 0;
}

Java

// Java Program to check if the point
// lies within the parabola or not

class solution
{

// Function to check the point
static int checkpoint(int h, int k, int x, int y, int a)
{
    // checking the equation of
    // parabola with the given point
    int p =(int) Math.pow((y - k), 2) - 4 * a * (x - h);

    return p;
}

//driver code
public static void main(String arr[])
{

    int h = 0, k = 0, x = 2, y = 1, a = 4;

    if (checkpoint(h, k, x, y, a) > 0)
    System.out.println("Outside");

    else if (checkpoint(h, k, x, y, a) == 0)
    System.out.println("On the parabola");

    else
    System.out.println("Inside");

}
}

Python3

# Python3 Program to check if the point
# lies within the parabola or not

#  Function to check the point
def checkpoint(h, k, x, y, a):

    # checking the equation of
    # parabola with the given point
    p = pow((y - k), 2) - 4 * a * (x - h)

    return p

# Driver code
if __name__ == "__main__" :

    h = 0
    k = 0
    x = 2
    y = 1
    a = 4

    if checkpoint(h, k, x, y, a) > 0:
        print ("Outside\n")

    elif checkpoint(h, k, x, y, a) == 0:
        print ("On the parabola\n")

    else:
        print ("Inside\n");

# This code is contributed by
# Surendra_Gangwar

C#

// C# Program to check if the point
// lies within the parabola or not
using System;

class GFG
{

// Function to check the point
public static int checkpoint(int h, int k,
                             int x, int y,
                             int a)
{
    // checking the equation of
    // parabola with the given point
    int p = (int) Math.Pow((y - k), 2) -
                            4 * a * (x - h);

    return p;
}

// Driver code
public static void Main(string[] arr)
{
    int h = 0, k = 0,
        x = 2, y = 1, a = 4;

    if (checkpoint(h, k, x, y, a) > 0)
    {
        Console.WriteLine("Outside");
    }

    else if (checkpoint(h, k, x, y, a) == 0)
    {
        Console.WriteLine("On the parabola");
    }

    else
    {
        Console.WriteLine("Inside");
    }
}
}

// This code is contributed
// by Shrikant13

PHP

<?php
// PHP Program to check if
// the point lies within
// the parabola or not

// Function to check the point
function checkpoint($h, $k, $x,
                        $y, $a)
{

    // checking the equation of
    // parabola with the given point
    $p = pow(($y - $k), 2) - 4 *
              $a * ($x - $h);

    return $p;
}

// Driver code
$h = 0; $k = 0; $x = 2;
$y = 1; $a = 4;

if (checkpoint($h, $k, $x,
               $y, $a) > 0)
    echo "Outside";
else if (checkpoint($h, $k, $x,
                    $y, $a) == 0)
    echo "On the parabola";
else
    echo "Inside";

// This code is contributed
// by inder_verma
?>

Javascript

<script>

// javascript Program to check if the point
// lies within the parabola or not

// Function to check the point
function checkpoint(h , k , x , y , a)
{
    // checking the equation of
    // parabola with the given point
    var p =parseInt(Math.pow((y - k), 2) - 4 * a * (x - h));

    return p;
}

//driver code
var h = 0, k = 0, x = 2, y = 1, a = 4;

if (checkpoint(h, k, x, y, a) > 0)
    document.write("Outside");

else if (checkpoint(h, k, x, y, a) == 0)
    document.write("On the parabola");

else
    document.write("Inside");

// This code is contributed by 29AjayKumar

</script>

Output:

Inside

Time Complexity: O(1)

Auxiliary Space: O(1)