Check if a point is inside, outside or on a Hyperbola
Last Updated :
25 Nov, 2021
Given a hyperbola centered at (h, k), with semi-major axis a, semi-minor axis b, both aligned with the Cartesian plane, the task is to determine if the point (x, y) lies within the area bounded by the hyperbola or not.

Examples:
Input: h = 0, k = 0, x = 2, y = 1, a = 4, b = 5
Output: Inside
Input: h = 1, k = 2, x = 200, y = 100, a = 6, b = 5
Output: Outside
Approach: The given problem can be solved by solving the equation of hyperbola mentioned below, for the given point (x, y):
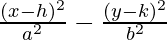
Based on the evaluated value of the above equation, the output of the program is as follows:
- Less than 1: The point lies inside the hyperbola.
- Equal to 1: The point lies on the hyperbola
- Greater than 1: The point lies outside the hyperbola.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void checkpoint(int h, int k, int x,
int y, int a, int b)
{
int p = (pow((x - h), 2) / pow(a, 2))
- (pow((y - k), 2) / pow(b, 2));
if (p > 1) {
cout << "Outside";
}
else if (p == 1) {
cout << "On the Hyperbola";
}
else {
cout << "Inside";
}
}
int main()
{
int h = 0, k = 0, x = 2;
int y = 1, a = 4, b = 5;
checkpoint(h, k, x, y, a, b);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG{
static void checkpoint(int h, int k, int x,
int y, int a, int b)
{
int p = (int)(Math.pow((x - h), 2) / Math.pow(a, 2)) -
(int)(Math.pow((y - k), 2) / Math.pow(b, 2));
if (p > 1)
{
System.out.println("Outside");
}
else if (p == 1)
{
System.out.println("On the Hyperbola");
}
else
{
System.out.println("Inside");
}
}
public static void main(String[] args)
{
int h = 0, k = 0, x = 2;
int y = 1, a = 4, b = 5;
checkpoint(h, k, x, y, a, b);
}
}
|
Python3
from math import pow
def checkpoint(h, k, x, y, a, b):
p = ((pow((x - h), 2) // pow(a, 2)) -
(pow((y - k), 2) // pow(b, 2)))
if (p > 1):
print("Outside")
elif (p == 1):
print("On the Hyperbola");
else:
print("Inside")
if __name__ == "__main__":
h = 0
k = 0
x = 2
y = 1
a = 4
b = 5
checkpoint(h, k, x, y, a, b)
|
C#
using System;
class GFG{
static void checkpoint(int h, int k, int x,
int y, int a, int b)
{
int p = (int)(Math.Pow((x - h), 2) / Math.Pow(a, 2)) -
(int)(Math.Pow((y - k), 2) / Math.Pow(b, 2));
if (p > 1)
{
Console.WriteLine("Outside");
}
else if (p == 1)
{
Console.WriteLine("On the Hyperbola");
}
else
{
Console.WriteLine("Inside");
}
}
public static void Main(string[] args)
{
int h = 0, k = 0, x = 2;
int y = 1, a = 4, b = 5;
checkpoint(h, k, x, y, a, b);
}
}
|
Javascript
<script>
function checkpoint(h, k, x, y, a, b)
{
p = ((Math.pow((x - h), 2) / Math.pow(a, 2)) -
(Math.pow((y - k), 2) / Math.pow(b, 2)))
if (p > 1)
console.log("Outside");
else if (p == 1)
console.log("On the Hyperbola");
else
console.log("Inside");
}
function main()
{
var h = 0;
var k = 0;
var x = 2;
var y = 1;
var a = 4;
var b = 5;
checkpoint(h, k, x, y, a, b);
}
main()
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...