Check if a number is Triperfect Number
Last Updated :
02 Jul, 2022
Given a number 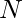 . The tasks is to check if the given number is a Triperfect Number.
. The tasks is to check if the given number is a Triperfect Number.
Triperfect Number: A Number is a Triperfect Number if it is equal to three times the sum of its divisors, that is, 3 times sum of its positive divisors.
Examples:
Input: N = 15
Output: false
Divisors of 15 are 1, 3, 5 and 15. Sum of
divisors is 24 which is not equal to 3*15 i.e. 45.
Input: N = 120
Output: true
Sum of divisors is 360 i.e. 3*120.
Hence 120 is a triperfect number.
A Simple Solution is to go through every number from 1 to N and check if it is a divisor. Maintain sum of all divisors. If sum becomes equal to 3*N, then return true, else return false.
An Efficient Solution is to go through numbers till square root of N. If a number ‘i’ divides n, then add both ‘i’ and n/i to sum.
Below is the implementation of the efficient approach:
C++
#include<bits/stdc++.h>
using namespace std;
bool isTriPerfect(int n )
{
int sum = 1 + n;
int i = 2;
while (i * i <= n)
{
if (n % i == 0)
{
if (n / i == i)
sum = sum + i;
else
sum = sum + i + n / i;
}
i += 1;
}
if (sum == 3 * n and n != 1)
return true;
else
false;
}
int main()
{
int n = 120;
if (isTriPerfect(n))
cout<<n<<" is a Triperfect number";
}
|
Java
public class GFG{
static boolean isTriPerfect(int n )
{
int sum = 1 + n;
int i = 2;
while (i * i <= n)
{
if (n % i == 0)
{
if (n / i == i)
sum = sum + i;
else
sum = sum + i + n / i;
}
i += 1;
}
if (sum == 3 * n & n != 1)
return true;
else
return false;
}
public static void main(String []args)
{
int n = 120;
if (isTriPerfect(n))
System.out.println(n + " is a Triperfect number");
}
}
|
Python3
def isTriPerfect( n ):
sum = 1 + n
i = 2
while i * i <= n:
if n % i == 0:
if n / i == i:
sum = sum + i
else:
sum = sum + i + n / i
i += 1
return (True if sum == 3 * n and n != 1 else False)
n = 120
if isTriPerfect (n):
print(n, "is a Triperfect number")
|
C#
using System;
public class GFG{
static bool isTriPerfect(int n )
{
int sum = 1 + n;
int i = 2;
while (i * i <= n)
{
if (n % i == 0)
{
if (n / i == i)
sum = sum + i;
else
sum = sum + i + n / i;
}
i += 1;
}
if (sum == 3 * n & n != 1)
return true;
else
return false;
}
public static void Main()
{
int n = 120;
if (isTriPerfect(n))
Console.WriteLine(n + " is a Triperfect number");
}
}
|
PHP
<?PHP
function isTriPerfect($n )
{
$sum = 1 + $n;
$i = 2;
while ($i * $i <= $n)
{
if ($n % $i == 0)
{
if ($n / $i == $i)
$sum = $sum + $i;
else
$sum = $sum + $i + $n / $i;
}
$i += 1;
}
if ($sum == 3 * $n and $n != 1)
return true;
else
false;
}
$n = 120;
if (isTriPerfect($n))
echo $n . " is a Triperfect number";
else
echo $n . " is not a Triperfect number";
?>
|
Javascript
<script>
function isTriPerfect(n)
{
let sum = 1 + n;
let i = 2;
while (i * i <= n)
{
if (n % i == 0)
{
if (parseInt(n / i, 10) == i)
sum = sum + i;
else
sum = sum + i + parseInt(n / i, 10);
}
i += 1;
}
if (sum == 3 * n & n != 1)
return true;
else
return false;
}
let n = 120;
if (isTriPerfect(n))
document.write(n + " is a Triperfect number");
</script>
|
Output: 120 is a Triperfect number
Time Complexity: O(log n)
Auxiliary Space: O(1)
Some interesting facts about TriPerfect Numbers:
- Till now only 6 Triperfect numbers are known. These are 120, 672, 523776, 459818240, 1476304896 and 51001180160.
- It has not been proven that more Triperfect Numbers don’t exist but it is believed that these are the only six.
Similarly, we can check for quad-perfect numbers(sum of factors = 4*n), five-perfect numbers( sum of factors = 5*n) and so on. There are currently 36 quad-perfect numbers known and 65 five-perfect numbers known.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...