Check if a number can be expressed as a product of exactly K prime divisors
Last Updated :
17 Nov, 2021
Given an integer N, the task is to check if it can be expressed as a product of exactly K prime divisors.
Examples:
Input: N = 12, K = 3
Output: Yes
Explanation:
12 can be expressed as product of 2×2×3.
Input: N = 14, K = 3
Output: No
Explanation:
14 can be only expressed as product of 2×7.
Approach:
To solve the problem mentioned above we are given the value N and we will find the maximum number of values we can split N into. We can represent prime factorization of N as 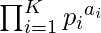 where pi are the prime factors of N and ai are the exponents. We know that total number of divisors of N is
where pi are the prime factors of N and ai are the exponents. We know that total number of divisors of N is 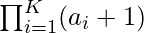 . Therefore, we can observe that we have to check whether it is possible to represent N as product of K numbers or not. If the maximum split is less than K then it is not possible to express it in exactly K prime divisors, else it is always possible.
. Therefore, we can observe that we have to check whether it is possible to represent N as product of K numbers or not. If the maximum split is less than K then it is not possible to express it in exactly K prime divisors, else it is always possible.
C++
#include <bits/stdc++.h>
using namespace std;
void KPrimeDivisors(int N, int K)
{
int maximum_split = 0;
while (N % 2 == 0) {
maximum_split++;
N /= 2;
}
for (int i = 3; i * i <= N; i = i + 2) {
while (N % i == 0) {
N = N / i;
maximum_split++;
}
}
if (N > 2)
maximum_split++;
if (maximum_split < K) {
printf("No\n");
return;
}
printf("Yes\n");
}
int main()
{
int N = 12;
int K = 3;
KPrimeDivisors(N, K);
return 0;
}
|
Java
class GFG {
static void KPrimeDivisors(int N, int K)
{
int maximum_split = 0;
while (N % 2 == 0) {
maximum_split++;
N /= 2;
}
for (int i = 3; i * i <= N; i = i + 2) {
while (N % i == 0) {
N = N / i;
maximum_split++;
}
}
if (N > 2)
maximum_split++;
if (maximum_split < K) {
System.out.println("No");
return;
}
System.out.println("Yes");
}
public static void main (String[] args)
{
int N = 12;
int K = 3;
KPrimeDivisors(N, K);
}
}
|
Python3
import math as mt
def KPrimeDivisors(n, k):
maximum_split = 0
while n % 2 == 0:
maximum_split+= 1
n = n // 2
for i in range(3, mt.ceil(mt.sqrt(n)), 2):
while n % i == 0:
n = n / i;
maximum_split+= 1
if n > 2:
maximum_split+= 1
if maximum_split < k:
print("No")
return
print("Yes")
N = 12
K = 3
KPrimeDivisors(N, K)
|
C#
using System;
class GFG {
static void KPrimeDivisors(int N, int K)
{
int maximum_split = 0;
while (N % 2 == 0) {
maximum_split++;
N /= 2;
}
for (int i = 3; i * i <= N; i = i + 2) {
while (N % i == 0) {
N = N / i;
maximum_split++;
}
}
if (N > 2)
maximum_split++;
if (maximum_split < K) {
Console.WriteLine("No");
return;
}
Console.WriteLine("Yes");
}
public static void Main(String[] args)
{
int N = 12;
int K = 3;
KPrimeDivisors(N, K);
}
}
|
Javascript
<script>
function KPrimeDivisors(N , K)
{
var maximum_split = 0;
while (N % 2 == 0)
{
maximum_split++;
N /= 2;
}
for (i = 3; i * i <= N; i = i + 2)
{
while (N % i == 0)
{
N = N / i;
maximum_split++;
}
}
if (N > 2)
maximum_split++;
if (maximum_split < K)
{
document.write("No");
return;
}
document.write("Yes");
}
var N = 12;
var K = 3;
KPrimeDivisors(N, K);
</script>
|
Time Complexity: O(sqrt(N))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...