Check if a Matrix is Invertible
Last Updated :
15 Jan, 2023
In linear algebra, an n-by-n square matrix A is called Invertible, if there exists an n-by-n square matrix B such that
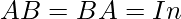
where ‘In‘ denotes the n-by-n identity matrix. The matrix B is called the inverse matrix of A.
A square matrix is Invertible if and only if its determinant is non-zero.
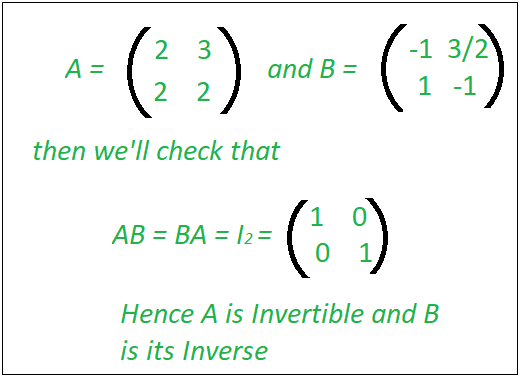
Examples:
Input : {{1, 2, 3}
{4, 5, 6}
{7, 8, 9}}
Output : No
The given matrix is NOT Invertible
The value of Determinant is: 0
We find determinant of the matrix. Then we check if the determinant value is 0 or not. If the value is 0, then we output, not invertible.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
#define N 4
void getCofactor(int mat[N][N], int temp[N][N], int p, int q, int n)
{
int i = 0, j = 0;
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
int determinantOfMatrix(int mat[N][N], int n)
{
int D = 0;
if (n == 1)
return mat[0][0];
int temp[N][N];
int sign = 1;
for (int f = 0; f < n; f++) {
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] * determinantOfMatrix(temp, n - 1);
sign = -sign;
}
return D;
}
bool isInvertible(int mat[N][N], int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
int main()
{
int mat[N][N] = { { 1, 0, 2, -1 },
{ 3, 0, 0, 5 },
{ 2, 1, 4, -3 },
{ 1, 0, 5, 0 } };
if (isInvertible(mat, N))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
class GFG
{
static int N = 4;
static void getCofactor(int [][]mat, int [][]temp,
int p, int q, int n)
{
int i = 0, j = 0;
for (int row = 0; row < n; row++)
{
for (int col = 0; col < n; col++)
{
if (row != p && col != q)
{
temp[i][j++] = mat[row][col];
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
static int determinantOfMatrix(int [][]mat,
int n)
{
int D = 0;
if (n == 1)
return mat[0][0];
int [][]temp = new int[N][N];
int sign = 1;
for (int f = 0; f < n; f++)
{
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] *
determinantOfMatrix(temp, n - 1);
sign = -sign;
}
return D;
}
static boolean isInvertible(int [][]mat, int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
public static void main(String []args)
{
int [][]mat = {{1, 0, 2, -1 },
{3, 0, 0, 5 },
{2, 1, 4, -3 },
{1, 0, 5, 0 }};
if (isInvertible(mat, N))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python 3
def getCofactor(mat, temp, p, q, n):
i = 0
j = 0
for row in range(n):
for col in range(n):
if (row != p and col != q) :
temp[i][j] = mat[row][col]
j += 1
if (j == n - 1):
j = 0
i += 1
def determinantOfMatrix(mat, n):
D = 0
if (n == 1):
return mat[0][0]
temp = [[0 for x in range(N)]
for y in range(N)]
sign = 1
for f in range(n):
getCofactor(mat, temp, 0, f, n)
D += (sign * mat[0][f] *
determinantOfMatrix(temp, n - 1))
sign = -sign
return D
def isInvertible(mat, n):
if (determinantOfMatrix(mat, N) != 0):
return True
else:
return False
mat = [[ 1, 0, 2, -1 ],
[ 3, 0, 0, 5 ],
[ 2, 1, 4, -3 ],
[ 1, 0, 5, 0 ]];
N = 4
if (isInvertible(mat, N)):
print("Yes")
else:
print("No")
|
C#
using System;
class GFG
{
static int N = 4;
static void getCofactor(int[,] mat, int[,] temp,
int p, int q, int n)
{
int i = 0, j = 0;
for (int row = 0; row < n; row++)
{
for (int col = 0; col < n; col++)
{
if (row != p && col != q)
{
temp[i, j++] = mat[row, col];
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
static int determinantOfMatrix(int[,]
mat, int n)
{
int D = 0;
if (n == 1)
return mat[0, 0];
int[,] temp = new int[N, N];
int sign = 1;
for (int f = 0; f < n; f++)
{
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0, f] *
determinantOfMatrix(temp, n - 1);
sign = -sign;
}
return D;
}
static bool isInvertible(int[,] mat, int n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
public static void Main()
{
int[,] mat = {{ 1, 0, 2, -1 },
{ 3, 0, 0, 5 },
{ 2, 1, 4, -3 },
{ 1, 0, 5, 0 }};
if (isInvertible(mat, N))
Console.Write("Yes");
else
Console.Write("No");
}
}
|
PHP
<?php
$N = 4;
function getCofactor(&$mat, &$temp,
$p, $q, $n)
{
$i = 0;
$j = 0;
for ($row = 0; $row < $n; $row++)
{
for ($col = 0; $col < $n; $col++)
{
if ($row != $p && $col != $q)
{
$temp[$i][$j++] = $mat[$row][$col];
if ($j == $n - 1)
{
$j = 0;
$i++;
}
}
}
}
}
function determinantOfMatrix(&$mat, $n)
{
$D = 0;
if ($n == 1)
return $mat[0][0];
$temp = array(array());
$sign = 1;
for ($f = 0; $f < $n; $f++)
{
getCofactor($mat, $temp, 0, $f, $n);
$D += $sign * $mat[0][$f] *
determinantOfMatrix($temp, $n - 1);
$sign = -$sign;
}
return $D;
}
function isInvertible(&$mat, $n)
{
global $N;
if (determinantOfMatrix($mat, $N) != 0)
return true;
else
return false;
}
$mat = array(array(1, 0, 2, -1 ),
array(3, 0, 0, 5 ),
array(2, 1, 4, -3 ),
array(1, 0, 5, 0 ));
if (isInvertible($mat, $N))
echo "Yes";
else
echo "No";
?>
|
Javascript
<script>
function getCofactor(mat,temp,p,q,n)
{
let i = 0, j = 0;
for (let row = 0; row < n; row++)
{
for (let col = 0; col < n; col++)
{
if (row != p && col != q)
{
temp[i][j++] = mat[row][col];
if (j == n - 1)
{
j = 0;
i++;
}
}
}
}
}
function determinantOfMatrix(mat,n)
{
let D = 0;
if (n == 1)
return mat[0][0];
let temp = new Array(N);
for(let i=0;i<N;i++)
{
temp[i]=new Array(N);
for(let j=0;j<N;j++)
{
temp[i][j]=0;
}
}
let sign = 1;
for (let f = 0; f < n; f++)
{
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f] *
determinantOfMatrix(temp, n - 1);
sign = -sign;
}
return D;
}
function isInvertible(mat,n)
{
if (determinantOfMatrix(mat, N) != 0)
return true;
else
return false;
}
let mat = [[ 1, 0, 2, -1 ],
[ 3, 0, 0, 5 ],
[ 2, 1, 4, -3 ],
[ 1, 0, 5, 0 ]];
let N = 4
if (isInvertible(mat, N))
document.write("Yes")
else
document.write("No")
</script>
|
Time Complexity: O(n3)
Auxiliary Space: O(n2)
Optimizing the Approach
If we extend the concept of calculating invertibility using a determinant from n =3 to some greater value, calculating the determinant would be quite cumbersome. Whether we do it using a pen and paper or use a calculator/computer.
So we’ll make use of the Reduced Row Echelon Form Concept. This makes use of computational operations which is quite efficient compared to the above-mentioned approach.
Here we’ll elaborate on the concept using a 4 X 4 matrix, which can be further generalized to an n X n matrix. The matrix will be processed by our function, replacing each row in turn and converting it to echelon form. We will return the value False if it ever fails because we can’t fit a 1 onto the leading diagonal; else, we will return True.
Approach:
Here is an implementation on Google Colab Notebook for the same.
import numpy as np #installing the numpy
The following steps need to be followed for a 4 X 4 matrix and can be generalized further for an N X N matrix.
- All we need for Row Zero is that the first element is equal to one.
- The row will be divided by the value of A[0, 0]. We’ll first check to see if A[0, 0] = 0, and if it does, we’ll add one of the lower rows to the first one before the division to avoid the problem.
- Until we can perform the division, we will repeat the test while moving down each lower row.
- The sub-diagonal elements will first be set to zero, or A[1,0].
- The diagonal component should then equal one. We’ll divide the row by A[1, 1]’s value.
- We must check one more to see if this is zero.
- If so, we will repeat the process of setting the sub-diagonal elements to zero and add a lower row.
- The same procedure continues further for the second and third row respectively.
Converting to Row Echelon Form
def isInvertible(X):
# Make Y as a copy of X, since we're going to alter it's values.
Y = np.array(X, dtype=np.float_)
try:
fix_r0(X)
fix_r1(X)
fix_r2(X)
fix_r3(X)
except MatrixIsSingular:
return False
return True
# The following line specifies our error flag.
# For if the matrix is singular and anything goes wrong.
class MatrixIsSingular(Exception):
pass
def fix_r0(A):
if A[0, 0] == 0:
A[0] = A[0] + A[1]
if A[0, 0] == 0:
A[0] = A[0] + A[2]
if A[0, 0] == 0:
A[0] = A[0] + A[3]
if A[0, 0] == 0:
raise MatrixIsSingular()
A[0] = A[0] / A[0, 0]
return A
def fix_r1(A):
A[1] = A[1] - A[1, 0] * A[0]
if A[1, 1] == 0:
A[1] = A[1] + A[2]
A[1] = A[1] - A[1, 0] * A[0]
if A[1, 1] == 0:
A[1] = A[1] + A[3]
A[1] = A[1] - A[1, 0] * A[0]
if A[1, 1] == 0:
raise MatrixIsSingular()
A[1] = A[1] / A[1, 1]
return A
def fix_r2(A):
# Set the sub-diagonal elements of row two to zero.
A[2] = A[2] - A[2, 0] * A[0]
A[2] = A[2] - A[2, 1] * A[1]
# Next we'll test that the diagonal element is not zero.
if A[2, 2] == 0:
A[2] = A[2] + A[3]
A[2] = A[2] - A[2, 0] * A[0]
A[2] = A[2] - A[2, 1] * A[1]
if A[2, 2] == 0:
raise MatrixIsSingular()
A[2] = A[2]/A[2, 2]
return A
def fix_r3(A):
# Set the sub-diagonal elements of row three to zero.
A[3] = A[3] - A[3, 0] * A[0]
A[3] = A[3] - A[3, 1] * A[1]
A[3] = A[3] - A[3, 2] * A[2]
if A[3, 3] == 0:
raise MatrixIsSingular()
# Transform the row to set the diagonal element to one.
A[3] = A[3]/A[3, 3]
return A
# Contributed by Pranav Gupta
Output1
Step-by-Step Demonstration:

Fixing Row 0
P.S. Performing this conversion on pen and paper might seem cumbersome but these approaches are made from the perspective of a machine and not a human. This is quite evident after watching the terms of the matrix after this step.
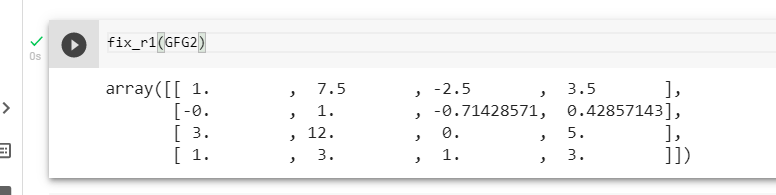
Fixing Row 1

Fixing Row 2
Finally, we arrived at our Reduced Row Echelon Form. As we can see We were able to reduce it to the desired form. Hence it is invertible. The code would have thrown the MatrixIsSingular exception and returned false if we had failed at any step. The memory required for the above approach would be O(1) as we are modifying just the copy of the original matrix in contrast to the naive approach which required additional O(n2) space for storing the co-factors. If the matrix is passed by the value we can perform the steps directly on the passed matrix.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...