Central binomial coefficient
Last Updated :
28 Jun, 2021
Given an integer N, the task is to find the 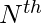 Central binomial coefficient.
Central binomial coefficient.
The first few Central binomial coefficients for N = 0, 1, 2, 3… are
1, 2, 6, 20, 70, 252, 924, 3432…..
Examples:
Input: N = 3
Output: 20
Explanation:
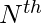 Central Binomial Coefficient =
Central Binomial Coefficient = 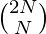 =
= 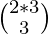 =
= 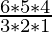 = 20
= 20
Input: N = 2
Output: 6
Approach: The central binomial coefficient is a binomial coefficient of the form 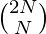 . The Binomial Coefficient
. The Binomial Coefficient 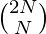 can be computed using this approach for a given value N using Dynamic Programming.
can be computed using this approach for a given value N using Dynamic Programming.
For Example:
Central binomial coefficient of N = 3 is given by:
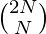 =
= 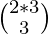 =
= 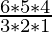 = 20
= 20
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k)
{
int C[n + 1][k + 1];
int i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
int main()
{
int n = 3;
int k = n;
n = 2*n;
cout << binomialCoeff(n, k);
}
|
Java
class GFG{
static int binomialCoeff(int n, int k)
{
int[][] C = new int[n + 1][k + 1];
int i, j;
for(i = 0; i <= n; i++)
{
for(j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
public static void main(String[] args)
{
int n = 3;
int k = n;
n = 2 * n;
System.out.println(binomialCoeff(n, k));
}
}
|
Python3
def binomialCoeff(n, k):
C = [[0 for j in range(k + 1)]
for i in range(n + 1)]
i = 0
j = 0
for i in range(n + 1):
for j in range(min(i, k) + 1):
if j == 0 or j == i:
C[i][j] = 1
else:
C[i][j] = (C[i - 1][j - 1] +
C[i - 1][j])
return C[n][k]
if __name__=='__main__':
n = 3
k = n
n = 2 * n
print(binomialCoeff(n, k))
|
C#
using System;
class GFG{
static int binomialCoeff(int n, int k)
{
int [,]C = new int[n + 1, k + 1];
int i, j;
for(i = 0; i <= n; i++)
{
for(j = 0; j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = C[i - 1, j - 1] +
C[i - 1, j];
}
}
return C[n, k];
}
public static void Main()
{
int n = 3;
int k = n;
n = 2 * n;
Console.Write(binomialCoeff(n, k));
}
}
|
Javascript
<script>
function binomialCoeff(n, k)
{
var C = Array.from(Array(n+1),()=> Array(k+1));
var i, j;
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
var n = 3;
var k = n;
n = 2*n;
document.write( binomialCoeff(n, k));
</script>
|
Time Complexity: O(N * K)
Auxiliary Space: O(N * K)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...