Centered triangular number

Given an integer n, find the nth Centered triangular number. 
Centered Triangular Number is a centered polygonal number that represents a triangle with a dot in the center and all other dots surrounding the center in successive triangular layers [Source : Wiki ]

Pictorial Representation :

The first few centered triangular number series are : 
1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460………………………..

Examples:

Input : n = 1
Output : 4
Explanation :
A dot in the center and 3 dots forming the
triangle outside it, thus 4.

Input : n = 6 
Output : 64

Input : n = 10
Output : 166

Approach
nth Term of centered triangular number is given by:  

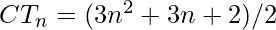
Basic Implementation of the above approach: 

C++

// C++ Program to find the
// nth Centered Triangular number
#include <iostream>
using namespace std;

// function for Centered
// Triangular number
int Centered_Triangular_num(int n)
{
    // formula for find Centered
    // Triangular number nth term
    return (3 * n * n + 3 * n + 2) / 2;
}

// Driver Code
int main()
{
    // For 3rd Centered Triangular number
    int n = 3;
    cout << Centered_Triangular_num(n) << endl;

    // For 12th Centered Triangular number
    n = 12;
    cout << Centered_Triangular_num(n) << endl;

    return 0;
}

C

// C Program to find the
// nth Centered Triangular number
#include <stdio.h>

// function for Centered
// Triangular number
int Centered_Triangular_num(int n)
{
    // formula for find Centered
    // Triangular number nth term
    return (3 * n * n + 3 * n + 2) / 2;
}

// Driver Code
int main()
{
    // For 3rd Centered Triangular number
    int n = 3;
    printf("%d\n",Centered_Triangular_num(n));

    // For 12th Centered Triangular number
    n = 12;
    printf("%d\n",Centered_Triangular_num(n));

    return 0;
}

// This code is contributed by kothavvsaakash.

Java

// Java Program to find
// the nth Centered
// Triangular number
import java.io.*;

class GFG
{

// function for Centered
// Triangular number
static int Centered_Triangular_num(int n)
{
    // formula for find Centered
    // Triangular number nth term
    return (3 * n * n +
            3 * n + 2) / 2;
}

// Driver Code
public static void main (String[] args)
{

// For 3rd Centered
// Triangular number
int n = 3;
System.out.println(Centered_Triangular_num(n));

// For 12th Centered
// Triangular number
n = 12;
System.out.println(Centered_Triangular_num(n));
}
}

// This code is contributed by ajit

Python3

# Program to find nth
# Centered Triangular number

def Centered_Triangular_num(n) :

    # Formula to calculate nth
    # Centered Triangular number
    return (3 * n * n +
            3 * n + 2) // 2

# Driver Code
if __name__ == '__main__' :

    # For 3rd Centered
    # Triangular number
    n = 3
    print(Centered_Triangular_num(n))

    # For 12th Centered
    # Triangular number
    n = 12
    print(Centered_Triangular_num(n))


# This code is contributed
# by akt_mit

C#

// C# Program to find
// the nth Centered
// Triangular number
using System;

class GFG
{

// function for Centered
// Triangular number
static int Centered_Triangular_num(int n)
{
    // formula for find Centered
    // Triangular number nth term
    return (3 * n * n +
            3 * n + 2) / 2;
}

// Driver Code
static public void Main ()
{

// For 3rd Centered
// Triangular number
int n = 3;
Console.WriteLine(Centered_Triangular_num(n));

// For 12th Centered
// Triangular number
n = 12;
Console.WriteLine(Centered_Triangular_num(n));
}
}

// This code is contributed by akt_mit

PHP

<?php
// PHP Program to find the
//nth Centered Triangular number

// function for Centered
// Triangular number
function Centered_Triangular_num($n)
{
    // formula for find Centered
    // Triangular number nth term
    return (3 * $n * $n + 3 * $n + 2) / 2;
}

// Driver Code
    // For 3rd Centered Triangular number
    $n = 3;
    echo Centered_Triangular_num($n), "\n" ;

    // For 12th Centered Triangular number
    $n = 12;
    echo Centered_Triangular_num($n), "\n";

// This code is contributed by aj_36
?>

Javascript

<script>
// javascript Program to find
// the nth Centered
// Triangular number

    // function for Centered
    // Triangular number
    function Centered_Triangular_num(n)
    {

        // formula for find Centered
        // Triangular number nth term
        return (3 * n * n + 3 * n + 2) / 2;
    }

    // Driver Code

        // For 3rd Centered
        // Triangular number
        var n = 3;
        document.write(Centered_Triangular_num(n)+"<br/>");

        // For 12th Centered
        // Triangular number
        n = 12;
        document.write(Centered_Triangular_num(n)+"<br/>");

// This code is contributed by Rajput-Ji
</script>

Output :

19
235

Time Complexity: O(1)
Auxiliary Space: O(1)