Cayley Table and Cyclic group | Mathematics
Last Updated :
20 May, 2019
Cayley Table –
If G is a finite group with the operation
*, the Cayley table of G is a table with rows and columns labeled by the elements of the group. The entry in the row labelled by and the column labeled by his the element g*h.
Example: Let’s construct the Cayley table of the group Z
5, the integers {0, 1, 2, 3, 4} under addition mod 5.
Step #1: We’ll label the rows and columns with the elements of Z
5, in the same order from left to right and top to bottom.
Step #2: We’ll fill in the table. Each entry is the result of adding the row label to the column label, then reducing mod 5.

Features of Cayley Table –
- Every row and column of the table should contain each element exactly once. If the table does not have this property, it can not represent a group; the cancellation law does not hold.
- The identity element of the group should not only appear in every row and column (exactly once), but it should also be “distributed symmetrically” about the main diagonal. Otherwise, one or more elements in the table do not have an inverse.
- There should not be any entries in the table that is not a row/column label. Otherwise, the operation is not closed.
- There should be one row in which the column labels appear in order, this indicates the presence of an identity element. The column of this element should reflect the row labels. Otherwise, there is no identity.
Note: If the Cayley table is symmetric along its diagonal then the group is an abelian group.
Cyclic group –
It is a group generated by a single element, and that element is called generator of that cyclic group. or a cyclic group G is one in which every element is a power of a particular element g, in the group. That is, every element of G can be written as g
n for some integer n for a multiplicative group, or ng for some integer n for an additive group. So, g is a generator of the group G.
Properties of Cyclic Group:
- Every cyclic group is also an Abelian group.
- If G is a cyclic group with generator g and order n. If m < n, then the order of the element gm is given by,
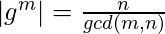
- Every subgroup of a cyclic group is cyclic.
- If G is a finite cyclic group with order n, the order of every element in G divides n.
- If d is a positive divisor of n, the number of elements of order d in a cyclic group of order n is Φ(d), where Φ(d) is Euler Phi function.
- The order of a cyclic group and the order of its generator is same.
Related GATE Questions:
1)
Gate CS 2004
2)
Gate CS 2009
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...