Can Run Time Complexity of a comparison-based sorting algorithm be less than N logN?
Last Updated :
13 Jul, 2022
Sorting algorithms are the means to sort a given set of data in an order according to the requirement of the user. They are primarily used to sort data in an increasing or decreasing manner. There are two types of sorting algorithms:
- Comparison-based sorting algorithms
- Non-comparison-based sorting algorithms
Comparison-based sorting algorithms: The elements of an array are compared to each other to sort the array. This type of algorithm checks if one element is greater than or equal to another element in the array. It does not do manipulation on a single array element.
Examples of comparison-based algorithms: Merge sort (compare the elements and copy them), Quicksort (compare the elements and swap them), and Heap sort (Heapify the elements using comparison).
Theorem: Every comparison-based sorting algorithm has the worst-case running time of 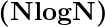
Proof:
Let us assume a comparison-based sorting algorithm, and an array of length N. Consider the input array contains array elements like 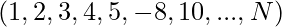 in some jumbled order. We can order these N elements in N! different ways.
in some jumbled order. We can order these N elements in N! different ways.
- Assumptions:
- 1st element has N ways of ordering, 2nd element has (N – 1) ways of ordering, 3rd element has (N – 2) ways, and so on.
So, these elements can be arranged in N! ways. - Let us suppose, the number of comparisons this algorithm makes in the worst case to arrange is K, i.e., the maximum number of comparisons on the N sized input array is K. To correctly sort all the N! possible inputs algorithm exhibits distinct executions.
- Proof: By the Pigeonhole principle: If n items are put into m containers, with n > m, then at least one container must contain more than one item.
- Here, the pigeon is N! different inputs. The holes are 2K different executions.
- If
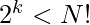 , this means the algorithm executes identically on 2 distinct inputs, and we can’t have a common execution of the sorting algorithm, which is averse to our assumption of a sorting algorithm.
, this means the algorithm executes identically on 2 distinct inputs, and we can’t have a common execution of the sorting algorithm, which is averse to our assumption of a sorting algorithm. - Since the sorting method is correct, 2K ≥ N! ≥ (N/2)N/2, Where we have used the fact that first N/2 terms of N*(N – 1)* … 2*1 are at least N/2.
- Taking log base 2 on both sides, K = (N/2)log2(N/2)
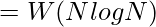
- Hence, every comparison-based sorting algorithm has the worst-case running time that can never be better than
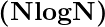 .
.
For more details, please refer:
Design and Analysis of Algorithms.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...