Can a function be equal to its inverse?

A function is a special type of relation or mapping between a given set of input values (called domain) and a set of outputs (called co-domain) where each value of the domain has a unique image in the co-domain (called range in this case). This means that an element of the domain can have only one image in the co-domain however two elements of the domain can have the same image. 

In case of a function every element of the domain has a unique image in co-domain.

The expression f : A⇢B means that f is a function  

An example of a function mapping.

Another example of function mapping

First image is a function and second image is not a function

The first image shows a function mapping whereas the second image is not a function because an element of domain has multiple images in co-domain.

Types of Functions

One-One function (injective): If every element of the domain has a distinct image in the co-domain, the function is said to be a one – one function.

Example of a one-one function.

Many-one function: In this case, multiple elements of the domain can have the same mapping in co-domain.

Example of a many-one function mapping.

Onto function (Surjection): When every element of the co domain has atleast one preimage in the domain the function is called Onto function.

An example of onto function.

Into function: In case there exists atleast one element in the co-domain that does not have a pre image in the domain it is said to be an Into function.

Into function

Bijective functions: A function that is both one-one and onto is known as a bijection.

Can a Function be equal to its Inverse?

Let’s suppose a given function y=f(x). the inverse of this function is represented by f^-1. it exists only when the given function is bijective. 

Consider a function f with a domain of X and a codomain of Y. Let’s suppose that there exists another function g. Now if the composition of these two functions that is f(g(x))=x then the two functions f and g are said to be inverses of each other.

This can be further generalized to check whether a given function is the inverse of itself. If the expression f(f(x))=x (also written as fof(x)=x) is true for any given function f then we can say that the function is the inverse of itself.

Consider a function y= f(x) is given.

Now as we know if the inverse of f(x) is f^-1(x) then

f^-1f(x) =x.

So for f(x) to be its own inverse. f^-1(x)=f(x)

From this we can conclude that when  f^-1(x)=f(x)

Then f(f(x)=x .

This can be applied on any function to check whether the function is its own inverse. 

Whenever a function is its own inverse we call it an involution or an involutory function.

Graphical Method

The graph of a function is a great way to know the nature of the function; by looking at it we can conclude its domain and its range and in some cases, we can know that function’s points of discontinuity. A graph is also helpful when we want to compare the values of two functions for the same domain value.   

Also, another way of checking whether a function is equal to its own inverse is by comparing the graph of the function with its inverse. Now if the graph of the function is the same as its inverse we can conclude that the function and its inverse are the same and the graph is an involution.

When the graph of a function is known the graph of its inverse can be found by taking its mirror image along the line y=x. So if we get the mirror image of the function the same as the actual function then we can say that the inverse of this function is the same as the function.

If we ever want to check if any function is its own inverse we can check its mirror image in the line y=x. If the reflection gives us the same function then its an inverse 

Sample Questions

Question 1: Check whether the linear function f(x)= 9 – x is its own inverse. 

Answer:

For checking if the function is the inverse of itself we apply the above mentioned operation on it

f(x) = 9 – x

fof(x) = 9 -(9 – x) = x

As seen above fof(x)=x for f(x)=9-x 

Therefore f is the inverse of itself.

Question 2: Check whether the following function is its own inverse. g(x)=(-x+2) / (5x+1).

Answer:

Given that,

g(x) = (-x+2) / (5x+1) 

gog(x)=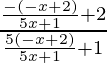

gog(x)=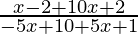

gog(x)=x.

Hence, the function g(x) is also it’s own inverse.

Question 3: Check whether the function h(x)=e^x cos x is its own inverse. 

Answer:

Given that,

h(x) = e^x cos x

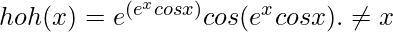
Thus, the function h(x) is not its own inverse.

Question 4: The function i(x)= ln (e^x+1) / (e^x+1) is given check if it is an involution.

Answer:

Given that, 

i(x) = ln (e^x+1) / (e^x+1)

ioi(x)=  .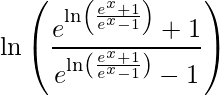

ioi(x)=  .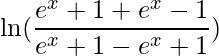

ioi(x)= x 

Thus the function i(x)=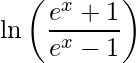is its own inverse.

Question 5: j(x)= sin x/(1 + cos x) is a function of x check whether it is it’s own inverse.

Answer:

Given that,

j(x) = sin x/(1 + cos x) 

j(x) = 2 sin (x/2) cos (x/2) / 1+(cos² (x/2) – sin² (x/2))

j(x) = tan(x/2)

joj(x) = tan(tan(x/2))

Thus, the function j(x) is not its own inverse.

Question 6: consider function f(x) = 9-x from above plot its graph and check if it is an involutory function

Answer:

Graph of function f(x) and y=x.

As you can see the reflection of f(x) along the line y=x yields the same graph as that of f(x). Hence for f(x) the function is equal to its inverse.

Question 2: Graphically check whether the function g(x) = (-x+2) / (5x + 1) is its own inverse.

Answer:

graph of g(x) and y=x

Since the graph of the function is symmetric along the line y=x it’s its own inverse.