Calculation of address of element of 1-D, 2-D, and 3-D using row-major and column-major order
Last Updated :
19 Apr, 2024
This article focuses on calculating the address of any element in a 1-Dimensional, 2-Dimensional, and 3-Dimensional array in Row major order and Column major order.
Calculating the address of any element In the 1-D array:
A 1-dimensional array (or single-dimension array) is a type of linear array. Accessing its elements involves a single subscript that can either represent a row or column index.
Example:
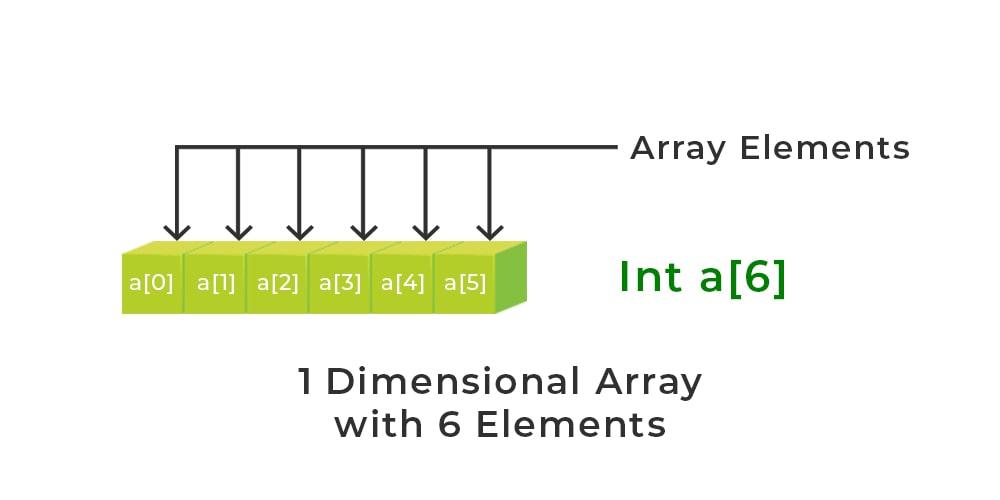
1-D array
To find the address of an element in an array the following formula is used-
Address of A[I] = B + W * (I – LB)
I = Subset of element whose address to be found,
B = Base address,
W = Storage size of one element store in any array(in byte),
LB = Lower Limit/Lower Bound of subscript(If not specified assume zero).
Example: Given the base address of an array A[1300 ………… 1900] as 1020 and the size of each element is 2 bytes in the memory, find the address of A[1700].
Solution:
Given:
Base address B = 1020
Lower Limit/Lower Bound of subscript LB = 1300
Storage size of one element store in any array W = 2 Byte
Subset of element whose address to be found I = 1700
Formula used:
Address of A[I] = B + W * (I – LB)
Solution:
Address of A[1700] = 1020 + 2 * (1700 – 1300)
= 1020 + 2 * (400)
= 1020 + 800
Address of A[1700] = 1820
Calculate the address of any element in the 2-D array:
The 2-dimensional array can be defined as an array of arrays. The 2-Dimensional arrays are organized as matrices which can be represented as the collection of rows and columns as array[M][N] where M is the number of rows and N is the number of columns.
Example:
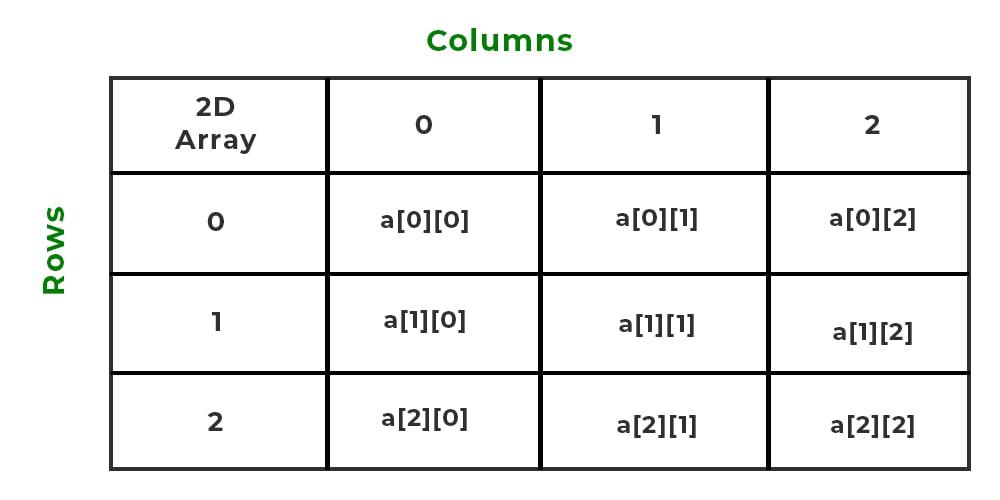
2-D array
To find the address of any element in a 2-Dimensional array there are the following two ways-
- Row Major Order
- Column Major Order
1. Row Major Order:
Row major ordering assigns successive elements, moving across the rows and then down the next row, to successive memory locations. In simple language, the elements of an array are stored in a Row-Wise fashion.
To find the address of the element using row-major order uses the following formula:
Address of A[I][J] = B + W * ((I – LR) * N + (J – LC))
I = Row Subset of an element whose address to be found,
J = Column Subset of an element whose address to be found,
B = Base address,
W = Storage size of one element store in an array(in byte),
LR = Lower Limit of row/start row index of the matrix(If not given assume it as zero),
LC = Lower Limit of column/start column index of the matrix(If not given assume it as zero),
N = Number of column given in the matrix.
Example: Given an array, arr[1………10][1………15] with base value 100 and the size of each element is 1 Byte in memory. Find the address of arr[8][6] with the help of row-major order.
Solution:
Given:
Base address B = 100
Storage size of one element store in any array W = 1 Bytes
Row Subset of an element whose address to be found I = 8
Column Subset of an element whose address to be found J = 6
Lower Limit of row/start row index of matrix LR = 1
Lower Limit of column/start column index of matrix = 1
Number of column given in the matrix N = Upper Bound – Lower Bound + 1
= 15 – 1 + 1
= 15
Formula:
Address of A[I][J] = B + W * ((I – LR) * N + (J – LC))
Solution:
Address of A[8][6] = 100 + 1 * ((8 – 1) * 15 + (6 – 1))
= 100 + 1 * ((7) * 15 + (5))
= 100 + 1 * (110)
Address of A[I][J] = 210
2. Column Major Order:
If elements of an array are stored in a column-major fashion means moving across the column and then to the next column then it’s in column-major order. To find the address of the element using column-major order use the following formula:
Address of A[I][J] = B + W * ((J – LC) * M + (I – LR))
I = Row Subset of an element whose address to be found,
J = Column Subset of an element whose address to be found,
B = Base address,
W = Storage size of one element store in any array(in byte),
LR = Lower Limit of row/start row index of matrix(If not given assume it as zero),
LC = Lower Limit of column/start column index of matrix(If not given assume it as zero),
M = Number of rows given in the matrix.
Example: Given an array arr[1………10][1………15] with a base value of 100 and the size of each element is 1 Byte in memory find the address of arr[8][6] with the help of column-major order.
Solution:
Given:
Base address B = 100
Storage size of one element store in any array W = 1 Bytes
Row Subset of an element whose address to be found I = 8
Column Subset of an element whose address to be found J = 6
Lower Limit of row/start row index of matrix LR = 1
Lower Limit of column/start column index of matrix = 1
Number of Rows given in the matrix M = Upper Bound – Lower Bound + 1
= 10 – 1 + 1
= 10
Formula: used
Address of A[I][J] = B + W * ((J – LC) * M + (I – LR))
Address of A[8][6] = 100 + 1 * ((6 – 1) * 10 + (8 – 1))
= 100 + 1 * ((5) * 10 + (7))
= 100 + 1 * (57)
Address of A[I][J] = 157
From the above examples, it can be observed that for the same position two different address locations are obtained that’s because in row-major order movement is done across the rows and then down to the next row, and in column-major order, first move down to the first column and then next column. So both the answers are right.
So it’s all based on the position of the element whose address is to be found for some cases the same answers is also obtained with row-major order and column-major order and for some cases, different answers are obtained.
Calculate the address of any element in the 3-D Array:
A 3-Dimensional array is a collection of 2-Dimensional arrays. It is specified by using three subscripts:
- Block size
- Row size
- Column size
More dimensions in an array mean more data can be stored in that array.
Example:
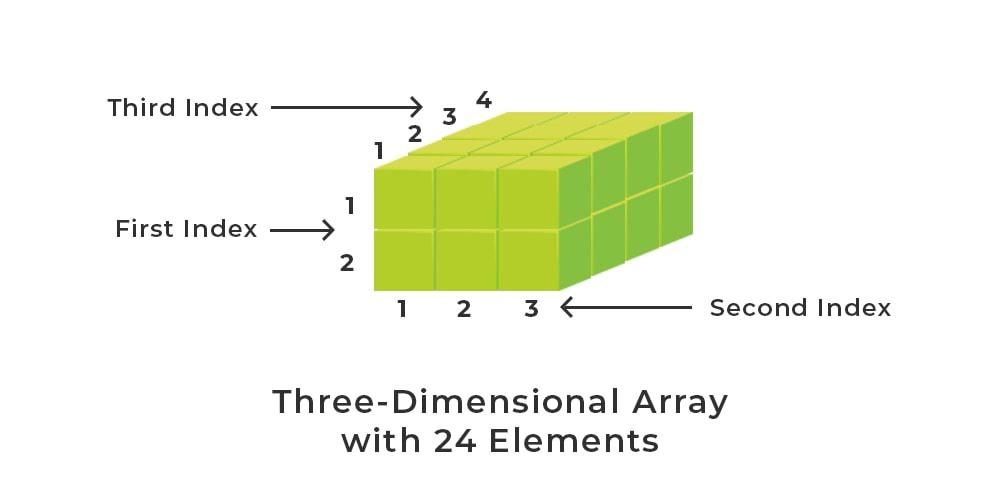
3-D array
To find the address of any element in 3-Dimensional arrays there are the following two ways-
- Row Major Order
- Column Major Order
1. Row Major Order:
To find the address of the element using row-major order, use the following formula:
Address of A[i][j][k] = B + W *(P* N * (i-x) + P*(j-y) + (k-z))
Here:
B = Base Address (start address)
W = Weight (storage size of one element stored in the array)
M = Row (total number of rows)
N = Column (total number of columns)
P = Width (total number of cells depth-wise)
x = Lower Bound of Row
y = Lower Bound of Column
z = Lower Bound of Width
Example: Given an array, arr[1:9, -4:1, 5:10] with a base value of 400 and the size of each element is 2 Bytes in memory find the address of element arr[5][-1][8] with the help of row-major order?
Solution:
Given:
Block Subset of an element whose address to be found I = 5
Row Subset of an element whose address to be found J = -1
Column Subset of an element whose address to be found K = 8
Base address B = 400
Storage size of one element store in any array(in Byte) W = 2
Lower Limit of blocks in matrix x = 1
Lower Limit of row/start row index of matrix y = -4
Lower Limit of column/start column index of matrix z = 5
M(row) = Upper Bound – Lower Bound + 1 = 1 – (-4) + 1 = 6
N(Column)= Upper Bound – Lower Bound + 1 = 10 – 5 + 1 = 6
Formula used:
Address of[I][J][K] =B + W (M * N(i-x) + N *(j-y) + (k-z))
Solution:
Address of arr[5][-1][8] = 400 + 2 * {[6 * 6 * (5 – 1)] + 6 * [(-1 + 4)]} + [8 – 5]
= 400 + 2 * (6*6*4)+(6*3)+3
= 400 + 2 * (165)
= 730
2. Column Major Order:
To find the address of the element using column-major order, use the following formula:1
Address of A[i][j][k]= B + W(M * N(i – x) + M *(k – z) + (j – y))
Here:
B = Base Address (start address)
W = Weight (storage size of one element stored in the array)
M = Row (total number of rows)
N = Column (total number of columns)
P = Width (total number of cells depth-wise)
x = Lower Bound of block (first subscipt)
y = Lower Bound of Row
z = Lower Bound of Column
Example: Given an array arr[1:8, -5:5, -10:5] with a base value of 400 and the size of each element is 4 Bytes in memory find the address of element arr[3][3][3] with the help of column-major order?
Solution:
Given:
Row Subset of an element whose address to be found I = 3
Column Subset of an element whose address to be found J = 3
Block Subset of an element whose address to be found K = 3
Base address B = 400
Storage size of one element store in any array(in Byte) W = 4
Lower Limit of blocks in matrix x = 1
Lower Limit of row/start row index of matrix y = -5
Lower Limit of column/start column index of matrix z = -10
M (row)= Upper Bound – Lower Bound + 1 = 5 +5 + 1 = 11
N (column)= Upper Bound – Lower Bound + 1 = 5 + 10 + 1 = 16
Formula used:
Address of A[i][j][k]=B+W×(M×P×(k−z)+M×(j−y)+(i−x))
Solution:
Address of arr[3][3][3] = 400 + 4 * ((11*16*(3-1)+11*(3-(-10)+(3-(-5)))
= 400 + 4 * ((176*2 + 11*13 + 8)
= 400 + 4 * (503)
= 400 + 2012
= 2412
Share your thoughts in the comments
Please Login to comment...