Calculate number of nodes between two vertices in an acyclic Graph by DFS method

Given a connected acyclic graph consisting of V vertices and E edges, a source vertex src, and a destination vertex dest, the task is to count the number of vertices between the given source and destination vertex in the graph.

Examples:

Input: V = 8, E = 7, src = 7, dest = 8, edges[][] ={{1 4}, {4, 5}, {4, 2}, {2, 6}, {6, 3}, {2, 7}, {3, 8}}
Output: 3
Explanation:
The path between 7 and 8 is 7 -> 2 -> 6 -> 3 -> 8.
So, the number of nodes between 7 and 8 is 3.
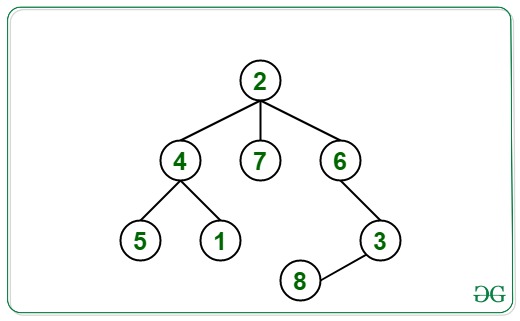
Input: V = 8, E = 7, src = 5, dest = 2, edges[][] ={{1 4}, {4, 5}, {4, 2}, {2, 6}, {6, 3}, {2, 7}, {3, 8}}
Output: 1
Explanation:
The path between 5 and 2 is 5 -> 4 -> 2.
So, the number of nodes between 5 and 2 is 1.

Approach: The problem can also be solved using the Disjoint Union method as stated in this article. Another approach to this problem is to solve using the Depth First Search method. Follow the steps below to solve this problem:

Initialize a visited array vis[] to mark which nodes are already visited. Mark all the nodes as 0, i.e., not visited.
Perform a DFS to find the number of nodes present in the path between src and dest.
The number of nodes between src and dest is equal to the difference between the length of the path between them and 2, i.e., (pathSrcToDest – 2).
Since the graph is acyclic and connected, there will always be a single path between src and dest.

Below is the implementation of the above algorithm.

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the count of nodes
// in the path from source to destination
int dfs(int src, int dest, int* vis,
        vector<int>* adj)
{
 
    // Mark the node visited
    vis[src] = 1;
 
    // If dest is reached
    if (src == dest) {
        return 1;
    }
 
    // Traverse all adjacent nodes
    for (int u : adj[src]) {
 
        // If not already visited
        if (!vis[u]) {
 
            int temp = dfs(u, dest, vis, adj);
 
            // If there is path, then
            // include the current node
            if (temp != 0) {
 
                return temp + 1;
            }
        }
    }
 
    // Return 0 if there is no path
    // between src and dest through
    // the current node
    return 0;
}
 
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
int countNodes(int V, int E, int src, int dest,
               int edges[][2])
{
    // Initialize an adjacency list
    vector<int> adj[V + 1];
 
    // Populate the edges in the list
    for (int i = 0; i < E; i++) {
        adj[edges[i][0]].push_back(edges[i][1]);
        adj[edges[i][1]].push_back(edges[i][0]);
    }
 
    // Mark all the nodes as not visited
    int vis[V + 1] = { 0 };
 
    // Count nodes in the path from src to dest
    int count = dfs(src, dest, vis, adj);
 
    // Return the nodes between src and dest
    return count - 2;
}
 
// Driver Code
int main()
{
    // Given number of vertices and edges
    int V = 8, E = 7;
 
    // Given source and destination vertices
    int src = 5, dest = 2;
 
    // Given edges
    int edges[][2]
        = { { 1, 4 }, { 4, 5 },
            { 4, 2 }, { 2, 6 },
            { 6, 3 }, { 2, 7 },
            { 3, 8 } };
 
    cout << countNodes(V, E, src, dest, edges);
 
    return 0;
}

Java

// Java program for the above approach
import java.util.Vector;
class GFG{
 
// Function to return the count of nodes
// in the path from source to destination
static int dfs(int src, int dest, int []vis,
               Vector<Integer> []adj)
{
  // Mark the node visited
  vis[src] = 1;
 
  // If dest is reached
  if (src == dest)
  {
    return 1;
  }
 
  // Traverse all adjacent nodes
  for (int u : adj[src])
  {
    // If not already visited
    if (vis[u] == 0)
    {
      int temp = dfs(u, dest,
                     vis, adj);
 
      // If there is path, then
      // include the current node
      if (temp != 0)
      {
        return temp + 1;
      }
    }
  }
 
  // Return 0 if there is no path
  // between src and dest through
  // the current node
  return 0;
}
 
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
static int countNodes(int V, int E,
                      int src, int dest,
                      int edges[][])
{
  // Initialize an adjacency list
  Vector<Integer> []adj = new Vector[V + 1];
  for (int i = 0; i < adj.length; i++)
    adj[i] = new Vector<Integer>();
   
  // Populate the edges in the list
  for (int i = 0; i < E; i++)
  {
    adj[edges[i][0]].add(edges[i][1]);
    adj[edges[i][1]].add(edges[i][0]);
  }
 
  // Mark all the nodes as
  // not visited
  int vis[] = new int[V + 1];
 
  // Count nodes in the path
  // from src to dest
  int count = dfs(src, dest,
                  vis, adj);
 
  // Return the nodes
  // between src and dest
  return count - 2;
}
 
// Driver Code
public static void main(String[] args)
{
  // Given number of vertices and edges
  int V = 8, E = 7;
 
  // Given source and destination vertices
  int src = 5, dest = 2;
 
  // Given edges
  int edges[][] = {{1, 4}, {4, 5},
                   {4, 2}, {2, 6},
                   {6, 3}, {2, 7},
                   {3, 8}};
 
  System.out.print(countNodes(V, E,
                              src, dest,
                              edges));
}
}
 
// This code is contributed by shikhasingrajput

Python3

# Python3 program for the above approach
 
# Function to return the count of nodes
# in the path from source to destination
def dfs(src, dest, vis, adj):
 
    # Mark the node visited
    vis[src] = 1
 
    # If dest is reached
    if (src == dest):
        return 1
 
    # Traverse all adjacent nodes
    for u in adj[src]:
 
        # If not already visited
        if not vis[u]:
            temp = dfs(u, dest, vis, adj)
 
            # If there is path, then
            # include the current node
            if (temp != 0):
                return temp + 1
 
    # Return 0 if there is no path
    # between src and dest through
    # the current node
    return 0
 
# Function to return the
# count of nodes between two
# given vertices of the acyclic Graph
def countNodes(V, E, src, dest, edges):
     
    # Initialize an adjacency list
    adj = [[] for i in range(V + 1)]
 
    # Populate the edges in the list
    for i in range(E):
        adj[edges[i][0]].append(edges[i][1])
        adj[edges[i][1]].append(edges[i][0])
 
    # Mark all the nodes as not visited
    vis = [0] * (V + 1)
 
    # Count nodes in the path from src to dest
    count = dfs(src, dest, vis, adj)
 
    # Return the nodes between src and dest
    return count - 2
 
# Driver Code
if __name__ == '__main__':
     
    # Given number of vertices and edges
    V = 8
    E = 7
 
    # Given source and destination vertices
    src = 5
    dest = 2
 
    # Given edges
    edges = [ [ 1, 4 ], [ 4, 5 ],
              [ 4, 2 ], [ 2, 6 ],
              [ 6, 3 ], [ 2, 7 ],
              [ 3, 8 ] ]
 
    print(countNodes(V, E, src, dest, edges))
 
# This code is contributed by mohit kumar 29   

C#

// C# program for
// the above approach
using System;
using System.Collections.Generic;
class GFG{
 
// Function to return the count of nodes
// in the path from source to destination
static int dfs(int src, int dest,
               int []vis, List<int> []adj)
{
  // Mark the node visited
  vis[src] = 1;
 
  // If dest is reached
  if (src == dest)
  {
    return 1;
  }
 
  // Traverse all adjacent nodes
  foreach (int u in adj[src])
  {
    // If not already visited
    if (vis[u] == 0)
    {
      int temp = dfs(u, dest,
                     vis, adj);
 
      // If there is path, then
      // include the current node
      if (temp != 0)
      {
        return temp + 1;
      }
    }
  }
 
  // Return 0 if there is no path
  // between src and dest through
  // the current node
  return 0;
}
 
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
static int countNodes(int V, int E,
                      int src, int dest,
                      int [,]edges)
{
  // Initialize an adjacency list
  List<int> []adj = new List<int>[V + 1];
   
  for (int i = 0; i < adj.Length; i++)
    adj[i] = new List<int>();
   
  // Populate the edges in the list
  for (int i = 0; i < E; i++)
  {
    adj[edges[i, 0]].Add(edges[i, 1]);
    adj[edges[i, 1]].Add(edges[i, 0]);
  }
 
  // Mark all the nodes as
  // not visited
  int []vis = new int[V + 1];
 
  // Count nodes in the path
  // from src to dest
  int count = dfs(src, dest,
                  vis, adj);
 
  // Return the nodes
  // between src and dest
  return count - 2;
}
 
// Driver Code
public static void Main(String[] args)
{
  // Given number of vertices and edges
  int V = 8, E = 7;
 
  // Given source and destination vertices
  int src = 5, dest = 2;
 
  // Given edges
  int [,]edges = {{1, 4}, {4, 5},
                  {4, 2}, {2, 6},
                  {6, 3}, {2, 7},
                  {3, 8}};
 
  Console.Write(countNodes(V, E, src,
                           dest, edges));
}
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
// Javascript program for the above approach
 
// Function to return the count of nodes
// in the path from source to destination
function dfs(src,dest,vis,adj)
{
  // Mark the node visited
  vis[src] = 1;
  
  // If dest is reached
  if (src == dest)
  {
    return 1;
  }
  
  // Traverse all adjacent nodes
  for (let u=0;u< adj[src].length;u++)
  {
    // If not already visited
    if (vis[adj[src][u]] == 0)
    {
      let temp = dfs(adj[src][u], dest,
                     vis, adj);
  
      // If there is path, then
      // include the current node
      if (temp != 0)
      {
        return temp + 1;
      }
    }
  }
  
  // Return 0 if there is no path
  // between src and dest through
  // the current node
  return 0;
}
 
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
function countNodes(V,E,src,dest,edges)
{
    // Initialize an adjacency list
  let adj = new Array(V + 1);
  for (let i = 0; i < adj.length; i++)
    adj[i] = [];
    
  // Populate the edges in the list
  for (let i = 0; i < E; i++)
  {
    adj[edges[i][0]].push(edges[i][1]);
    adj[edges[i][1]].push(edges[i][0]);
  }
  
  // Mark all the nodes as
  // not visited
  let vis = new Array(V + 1);
  for(let i=0;i<vis.length;i++)
  {
      vis[i]=0;
  }
  // Count nodes in the path
  // from src to dest
  let count = dfs(src, dest,
                  vis, adj);
  
  // Return the nodes
  // between src and dest
  return count - 2;
}
 
// Driver Code
// Given number of vertices and edges
let V = 8, E = 7;
 
// Given source and destination vertices
let src = 5, dest = 2;
 
// Given edges
let edges = [[1, 4], [4, 5],
[4, 2], [2, 6],
[6, 3], [2, 7],
[3, 8]];
 
document.write(countNodes(V, E,
                            src, dest,
                            edges));
 
 
// This code is contributed by unknown2108
</script>