Calculate number of nodes in all subtrees | Using DFS
Last Updated :
18 Sep, 2023
Given a tree in the form of adjacency list we have to calculate the number of nodes in the subtree of each node while calculating the number of nodes in the subtree of a particular node that node will also be added as a node in subtree hence the number of nodes in subtree of leaves is 1.
Examples:
Input : Consider the Graph mentioned below:
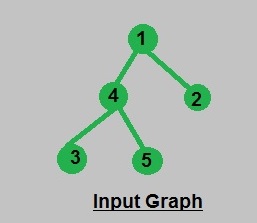
Output : Nodes in subtree of 1 : 5
Nodes in subtree of 2 : 1
Nodes in subtree of 3 : 1
Nodes in subtree of 4 : 3
Nodes in subtree of 5 : 1
Input : Consider the Graph mentioned below:
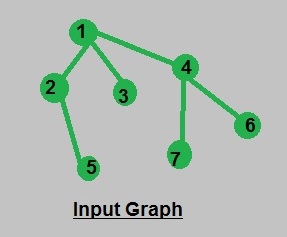
Output : Nodes in subtree of 1 : 7
Nodes in subtree of 2 : 2
Nodes in subtree of 3 : 1
Nodes in subtree of 4 : 3
Nodes in subtree of 5 : 1
Nodes in subtree of 6 : 1
Nodes in subtree of 7 : 1
Explanation: First we should calculate value count[s] : the number of nodes in subtree of node s. Where subtree contains the node itself and all the nodes in the subtree of its children. Thus, we can calculate the number of nodes recursively using the concept of DFS and DP, where we should process each edge only once and count[] value of children used in calculating count[] of its parent expressing the concept of DP(Dynamic programming).
Time Complexity : O(n) [in processing of all (n-1) edges].
Algorithm :
void numberOfNodes(int s, int e)
{
vector::iterator u;
count1[s] = 1;
for (u = adj[s].begin(); u != adj[s].end(); u++)
{
// condition to omit reverse path
// path from children to parent
if (*u == e)
continue;
// recursive call for DFS
numberOfNodes(*u, s);
// update count[] value of parent using
// its children
count1[s] += count1[*u];
}}
Implementation:
C++
Java
Python3
N = 8
count1 = [0] * (N)
adj = [[] for i in range(N)]
def numberOfNodes(s, e):
count1[s] = 1
for u in adj[s]:
if u == e:
continue
numberOfNodes(u, s)
count1[s] += count1[u]
def addEdge(a, b):
adj[a].append(b)
adj[b].append(a)
def printNumberOfNodes():
for i in range(1, N):
print("Nodes in subtree of", i,
":", count1[i])
if __name__ == "__main__":
addEdge(1, 2)
addEdge(1, 4)
addEdge(1, 5)
addEdge(2, 6)
addEdge(4, 3)
addEdge(4, 7)
numberOfNodes(1, 0)
printNumberOfNodes()
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static readonly int N = 8;
static int []count1 = new int[N];
static List<int> []adj = new List<int>[N];
static void numberOfNodes(int s, int e)
{
count1[s] = 1;
foreach(int u in adj[s])
{
if(u == e)
continue;
numberOfNodes(u, s);
count1[s] += count1[u];
}
}
static void addEdge(int a, int b)
{
adj[a].Add(b);
adj[b].Add(a);
}
static void printNumberOfNodes()
{
for (int i = 1; i < N; i++)
Console.WriteLine("Node of a subtree of "+ i +
" : "+ count1[i]);
}
public static void Main(String[] args)
{
for(int i = 0; i < N; i++)
adj[i] = new List<int>();
addEdge(1, 2);
addEdge(1, 4);
addEdge(1, 5);
addEdge(2, 6);
addEdge(4, 3);
addEdge(4, 7);
numberOfNodes(1, 0);
printNumberOfNodes();
}
}
|
Javascript
<script>
let N = 8;
let count1 = new Array(N);
let adj = new Array(N);
function numberOfNodes(s, e)
{
count1[s] = 1;
for(let u = 0; u < adj[s].length; u++)
{
if(adj[s][u] == e)
continue;
numberOfNodes(adj[s][u] ,s);
count1[s] += count1[adj[s][u]];
}
}
function addEdge(a, b)
{
adj[a].push(b);
adj[b].push(a);
}
function printNumberOfNodes()
{
for (let i = 1; i < N; i++)
document.write("Node of a subtree of "+ i+
" : "+ count1[i] + "</br>");
}
for(let i = 0; i < N; i++)
adj[i] = [];
addEdge(1, 2);
addEdge(1, 4);
addEdge(1, 5);
addEdge(2, 6);
addEdge(4, 3);
addEdge(4, 7);
numberOfNodes(1, 0);
printNumberOfNodes();
</script>
|
Output
Nodes in subtree of 1: 7
Nodes in subtree of 2: 2
Nodes in subtree of 3: 1
Nodes in subtree of 4: 3
Nodes in subtree of 5: 1
Nodes in subtree of 6: 1
Nodes in subtree of 7: 1
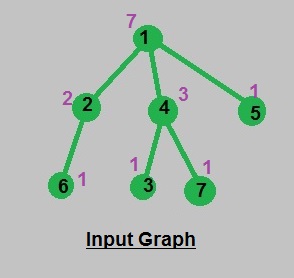
Input and Output illustration:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...