Calculate determinant of a Matrix using Pivotal Condensation Method

Given a square matrix mat[][] of dimension N, the task is to find the determinant of the matrix using the pivot condensation method.

Examples:

Input: mat[][] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
Output: 0
Explanation:
Performing R3 = R3 – R2 modifies the matrix mat[][] to {{1, 2, 3}, {4, 5, 6}, {1, 1, 1}}.
Performing R2 = R2 – R1 modifies the matrix mat[][] to {{1, 2, 3}, {1, 1, 1}, {1, 1, 1}}.
Now, the rows R2 and R3 are equal.
Therefore, the determinant will of the matrix becomes equal to zero (using the property of matrix).

Input: mat[][] = {{1, 0, 2, -1}, {3, 0, 0, 5}, {2, 1, 4, -3}, {1, 0, 5, 0}}
Output: 30

Approach: The idea is to use the Pivotal Condensation method to calculate the determinant of the matrix mat[][]. Below is the detailed explanation of the proposed method:

In this method of calculating the determinant of dimension N × N, square matrix:

• First the matrix A[][] of dimension N*N is reduced to matrix B[][] of dimension (N – 1)*(N – 1) such that:

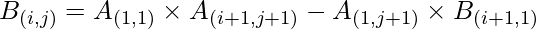
• Then the determinant value of A[][] can be found out from matrix B[][] using the formula,

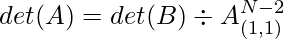
• Now further reduce the matrix to (N – 2)*(N – 2) and calculate the determinant of matrix B[][].
• And repeat the above process until the matrix becomes of dimension 2*2.
• Then the determinant of the matrix of dimension 2×2 is calculated using formula det(A) = ad-bc for a matrix say A[][] as {{a, b}, {c, d}}.

Follow the steps below to solve the problem:

• Initialize a variable, say D, to store the determinant of the matrix.
• Iterate while N is greater than 2 and check for the following:
  • Check if mat[0][0] is 0, then swap the current row with the next row such that mat[i][0] > 0 using the property of matrix.
  • Otherwise, if no row is found such that mat[i][0] > 0, then print zero.
  • Now, multiply D by pow(1 / mat[0][0], N – 2).
  • Calculate the next matrix, say B[][], of dimension (N – 1) x (N – 1) using the formula b[i – 1][j – 1] = mat[0][0 * mat[i][i] – mat[0][j] * mat[i][0].
  • Assign mat = B.
• Multiply D by the determinant of the matrix mat[][] of dimension 2×2, i.e mat[0][0] * mat[1][1] – mat[0][j] * mat[i][0].
• Finally, print the value stored in D.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to swap values
void swap(float& i, float& j)
{
    float temp = i;
    i = j;
    j = temp;
}

// Function to find the determinant
// of matrix M[][]
float determinantOfMatrix(
    vector<vector<float> > mat, int N)
{
    float mul = 1;

    // Iterate over N while N > 2
    while (N > 2) {

        // Store the reduced matrix
        // of dimension (N-1)x(N-1)
        float M[N - 1][N - 1];

        int next_index = 1;

        // Check if first element
        // of first row is zero
        while (mat[0][0] == 0) {

            if (mat[next_index][0] > 0) {

                // For swapping
                for (int k = 0; k < N; k++) {
                    swap(mat[0][k],
                         mat[next_index][k]);
                }

                // Update mul
                mul = mul * pow((-1),
                                (next_index));
            }

            else if (next_index == (N - 1))
                return 0;
            next_index++;
        }

        // Store the first element
        // of the matrix
        float p = mat[0][0];

        // Multiply the mul by
        // (1/p) to the power n-2
        mul = mul * pow(1 / p, N - 2);

        // Calculate the next matrix
        // of dimension (N-1) x (N-1)
        for (int i = 1; i < N; i++) {
            for (int j = 1; j < N; j++) {

                // Calculate each element of
                // the matrix from previous
                // matrix
                M[i - 1][j - 1] = mat[0][0]
                                      * mat[i][j]
                                  - mat[i][0]
                                        * mat[0][j];
            }
        }

        // Copy elements of the matrix
        // M into mat to use it in
        // next iteration
        for (int i = 0;
             i < (N - 1); i++) {

            for (int j = 0;
                 j < (N - 1); j++) {

                mat[i][j] = M[i][j];
            }
        }

        // Decrement N by one
        N--;
    }

    // Calculate the determinant
    // of reduced 2x2 matrix and
    // multiply it with factor mul
    float D = mul * (mat[0][0]
                         * mat[1][1]
                     - mat[0][1]
                           * mat[1][0]);

    // Print the determinant
    cout << D;
}

// Driver Code
int main()
{
    // Given matrix
    vector<vector<float> > mat = { { 1, 0, 2, -1 },
                                   { 3, 0, 0, 5 },
                                   { 2, 1, 4, -3 },
                                   { 1, 0, 5, 0 } };

    // Size of the matrix
    int N = mat.size();

    // Function Call
    determinantOfMatrix(mat, N);

    return 0;
}

Java

// Java program for the above approach
import java.util.*;
class GFG
{

// Function to find the determinant
// of matrix M[][]
static void determinantOfMatrix(int[][] mat, int N)
{
    int mul = 1;

    // Iterate over N while N > 2
    while (N > 2)
    {

        // Store the reduced matrix
        // of dimension (N-1)x(N-1)
        int [][]M = new int[N - 1][N - 1];
        int next_index = 1;

        // Check if first element
        // of first row is zero
        while (mat[0][0] == 0)
        {
            if (mat[next_index][0] > 0)
            {

                // For swapping
                for (int k = 0; k < N; k++)
                {
                    int temp = mat[0][k];
                    mat[0][k] = mat[next_index][k];
                    mat[next_index][k] = temp;

                }

                // Update mul
                mul = (int) (mul * Math.pow((-1),
                                (next_index)));
            }
            else if (next_index == (N - 1))
                return;
            next_index++;
        }

        // Store the first element
        // of the matrix
        int p = mat[0][0];

        // Multiply the mul by
        // (1/p) to the power n-2
        mul = (int) (mul * Math.pow(1 / p, N - 2));

        // Calculate the next matrix
        // of dimension (N-1) x (N-1)
        for (int i = 1; i < N; i++)
        {
            for (int j = 1; j < N; j++)
            {

                // Calculate each element of
                // the matrix from previous
                // matrix
                M[i - 1][j - 1] = mat[0][0]
                                      * mat[i][j]
                                  - mat[i][0]
                                        * mat[0][j];
            }
        }

        // Copy elements of the matrix
        // M into mat to use it in
        // next iteration
        for (int i = 0;
             i < (N - 1); i++)
        {
            for (int j = 0;
                 j < (N - 1); j++)
            {
                mat[i][j] = M[i][j];
            }
        }

        // Decrement N by one
        N--;
    }

    // Calculate the determinant
    // of reduced 2x2 matrix and
    // multiply it with factor mul
    int D = mul * (mat[0][0]
                         * mat[1][1]
                     - mat[0][1]
                           * mat[1][0]);

    // Print the determinant
    System.out.print(D);
}

// Driver Code
public static void main(String[] args)
{

    // Given matrix
    int[][] mat = { { 1, 0, 2, -1 },
                                   { 3, 0, 0, 5 },
                                   { 2, 1, 4, -3 },
                                   { 1, 0, 5, 0 } };

    // Size of the matrix
    int N = mat.length;

    // Function Call
    determinantOfMatrix(mat, N);
}
}

// This code is contributed by 29AjayKumar

Python3

# Python 3 program for the above approach

# Function to find the determinant
# of matrix M[][]
def determinantOfMatrix(mat, N):
    mul = 1

    # Iterate over N while N > 2
    while (N > 2):
        # Store the reduced matrix
        # of dimension (N-1)x(N-1)
        M = [[0 for i in range(N-1)] for j in range(N-1)]

        next_index = 1

        # Check if first element
        # of first row is zero
        while (mat[0][0] == 0):
            if (mat[next_index][0] > 0):
                # For swapping
                for k in range(N):
                    temp = mat[0][k]
                    mat[0][k] = mat[next_index][k]
                    mat[next_index][k] = temp

                # Update mul
                mul = mul * pow((-1),(next_index))

            elif (next_index == (N - 1)):
                return 0;
            next_index += 1

        # Store the first element
        # of the matrix
        p = mat[0][0]

        # Multiply the mul by
        # (1/p) to the power n-2
        mul = mul * pow(1 / p, N - 2)

        # Calculate the next matrix
        # of dimension (N-1) x (N-1)
        for i in range(1,N):
            for j in range(1,N,1):
                # Calculate each element of
                # the matrix from previous
                # matrix
                M[i - 1][j - 1] = mat[0][0] * mat[i][j] - mat[i][0] * mat[0][j]

        # Copy elements of the matrix
        # M into mat to use it in
        # next iteration
        for i in range(N - 1):
            for j in range(N - 1):
                mat[i][j] = M[i][j]

        # Decrement N by one
        N -= 1

    # Calculate the determinant
    # of reduced 2x2 matrix and
    # multiply it with factor mul
    D = mul * (mat[0][0] * mat[1][1] - mat[0][1] * mat[1][0])

    # Print the determinant
    print(int(D))

# Driver Code
if __name__ == '__main__':
    # Given matrix
    mat = [[1, 0, 2, -1],[3, 0, 0, 5], [2, 1, 4, -3], [1, 0, 5, 0]]

    # Size of the matrix
    N = len(mat)

    # Function Call
    determinantOfMatrix(mat, N)

    # This code is contributed by bgangwar59.

C#

// C# program for the above approach
using System;

public class GFG
{

// Function to find the determinant
// of matrix [,]M
static void determinantOfMatrix(int[,] mat, int N)
{
    int mul = 1;

    // Iterate over N while N > 2
    while (N > 2)
    {

        // Store the reduced matrix
        // of dimension (N-1)x(N-1)
        int [,]M = new int[N - 1,N - 1];
        int next_index = 1;

        // Check if first element
        // of first row is zero
        while (mat[0,0] == 0)
        {
            if (mat[next_index,0] > 0)
            {

                // For swapping
                for (int k = 0; k < N; k++)
                {
                    int temp = mat[0,k];
                    mat[0,k] = mat[next_index,k];
                    mat[next_index,k] = temp;

                }

                // Update mul
                mul = (int) (mul * Math.Pow((-1),
                                (next_index)));
            }
            else if (next_index == (N - 1))
                return;
            next_index++;
        }

        // Store the first element
        // of the matrix
        int p = mat[0,0];

        // Multiply the mul by
        // (1/p) to the power n-2
        mul = (int) (mul * Math.Pow(1 / p, N - 2));

        // Calculate the next matrix
        // of dimension (N-1) x (N-1)
        for (int i = 1; i < N; i++)
        {
            for (int j = 1; j < N; j++)
            {

                // Calculate each element of
                // the matrix from previous
                // matrix
                M[i - 1,j - 1] = mat[0,0]
                                      * mat[i,j]
                                  - mat[i,0]
                                        * mat[0,j];
            }
        }

        // Copy elements of the matrix
        // M into mat to use it in
        // next iteration
        for (int i = 0;
             i < (N - 1); i++)
        {
            for (int j = 0;
                 j < (N - 1); j++)
            {
                mat[i,j] = M[i,j];
            }
        }

        // Decrement N by one
        N--;
    }

    // Calculate the determinant
    // of reduced 2x2 matrix and
    // multiply it with factor mul
    int D = mul * (mat[0,0]
                         * mat[1,1]
                     - mat[0,1]
                           * mat[1,0]);

    // Print the determinant
    Console.Write(D);
}

// Driver Code
public static void Main(String[] args)
{

    // Given matrix
    int[,] mat = { { 1, 0, 2, -1 },
                                   { 3, 0, 0, 5 },
                                   { 2, 1, 4, -3 },
                                   { 1, 0, 5, 0 } };

    // Size of the matrix
    int N = mat.GetLength(0);

    // Function Call
    determinantOfMatrix(mat, N);
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>
    // Javascript program for the above approach

    // Function to find the determinant
    // of matrix M[][]
    function determinantOfMatrix(mat, N)
    {
        let mul = 1;

        // Iterate over N while N > 2
        while (N > 2)
        {

            // Store the reduced matrix
            // of dimension (N-1)x(N-1)
            let M = new Array(N - 1);
            for(let i = 0; i < N - 1; i++)
            {
                M[i] = new Array(N - 1);
                for(let j = 0; j < N - 1; j++)
                {
                    M[i][j] = 0;
                }
            }
            let next_index = 1;

            // Check if first element
            // of first row is zero
            while (mat[0][0] == 0)
            {
                if (mat[next_index][0] > 0)
                {

                    // For swapping
                    for (let k = 0; k < N; k++)
                    {
                        let temp = mat[0][k];
                        mat[0][k] = mat[next_index][k];
                        mat[next_index][k] = temp;

                    }

                    // Update mul
                    mul = (mul * Math.pow((-1),
                                    (next_index)));
                }
                else if (next_index == (N - 1))
                    return;
                next_index++;
            }

            // Store the first element
            // of the matrix
            let p = mat[0][0];

            // Multiply the mul by
            // (1/p) to the power n-2
            mul = (mul * Math.pow(parseInt(1 / p, 10), N - 2));

            // Calculate the next matrix
            // of dimension (N-1) x (N-1)
            for (let i = 1; i < N; i++)
            {
                for (let j = 1; j < N; j++)
                {

                    // Calculate each element of
                    // the matrix from previous
                    // matrix
                    M[i - 1][j - 1] = mat[0][0]
                                          * mat[i][j]
                                      - mat[i][0]
                                            * mat[0][j];
                }
            }

            // Copy elements of the matrix
            // M into mat to use it in
            // next iteration
            for (let i = 0;
                 i < (N - 1); i++)
            {
                for (let j = 0;
                     j < (N - 1); j++)
                {
                    mat[i][j] = M[i][j];
                }
            }

            // Decrement N by one
            N--;
        }

        // Calculate the determinant
        // of reduced 2x2 matrix and
        // multiply it with factor mul
        let D = mul * (mat[0][0]
                             * mat[1][1]
                         - mat[0][1]
                               * mat[1][0]);

        // Print the determinant
        document.write(D);
    }

    // Given matrix
    let mat = [ [ 1, 0, 2, -1 ],
               [ 3, 0, 0, 5 ],
               [ 2, 1, 4, -3 ],
               [ 1, 0, 5, 0 ] ];

    // Size of the matrix
    let N = mat.length;

    // Function Call
    determinantOfMatrix(mat, N);

// This code is contributed by decode2207.
</script>

Output:

30

Time Complexity: O(N³)
Auxiliary Space: O(N²)