Calculate area of pentagon with given diagonal
Last Updated :
24 Jun, 2022
Given an integer d which is the length of the diagonal of a pentagon, the task is to find the area of that pentagon.

Examples:
Input: d = 5
Output: 16.4291
Input: d = 10
Output: 65.7164
Approach: Pentagon is a regular polygon having five equal sides and all equal angles. The interior angles of pentagon are of 108 degrees each and the sum of all angles of a pentagon is 540 degrees. If d is the diagonal of the pentagon then it’s area is given by:
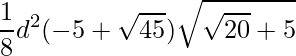
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float pentagonArea(float d)
{
float area;
area = (d * d * (-5 + sqrt(45)) * sqrt(sqrt(20) + 5)) / 8;
return area;
}
int main()
{
float d = 5;
cout << pentagonArea(d);
return 0;
}
|
Java
import java.text.*;
class GFG{
static double pentagonArea(double d)
{
double area;
area = (d * d * (-5 + Math.sqrt(45)) * Math.sqrt(Math.sqrt(20) + 5)) / 8;
return area;
}
public static void main(String[] args)
{
double d = 5;
DecimalFormat dec = new DecimalFormat("#0.0000");
System.out.println(dec.format(pentagonArea(d)));
}
}
|
Python3
from math import sqrt
def pentagonArea(d) :
area = (d * d * (-5 + sqrt(45)) * sqrt(sqrt(20) + 5)) / 8
return round(area , 4)
if __name__ == "__main__" :
d = 5
print(pentagonArea(d))
|
C#
using System;
class GFG{
static double pentagonArea(double d)
{
double area;
area = (d * d * (-5 + Math.Sqrt(45)) * Math.Sqrt(Math.Sqrt(20) + 5)) / 8;
return area;
}
public static void Main()
{
double d = 5;
Console.WriteLine("{0:F4}",pentagonArea(d));
}
}
|
PHP
<?php
Function pentagonArea($d)
{
$area;
$area= ($d * $d * (-5 +sqrt(45)) * sqrt(sqrt(20) + 5)) / 8;
return $area;
}
{
$d = 5;
echo(pentagonArea($d));
return 0;
}
|
Javascript
<script>
function pentagonArea( d)
{
let area;
area = (d * d * (-5 + Math.sqrt(45)) * Math.sqrt(Math.sqrt(20) + 5)) / 8;
return area;
}
let d = 5;
document.write(pentagonArea(d).toFixed(4));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...