Transpose of a Matrix in C

In this article, we will learn how to write a C program to find the transpose of a matrix. The transpose of a matrix is a new matrix formed by interchanging its rows with columns. In simple words, the transpose of A[][] is obtained by changing A[i][j] to A[j][i].

Note: The transpose of an m × n matrix will result in an n × m matrix.

Example

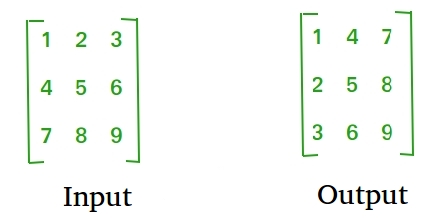
Algorithm to Find the Transpose of a Matrix

The idea is to run a nested loop and copy the elements of the original matrix A to the resultant matrix B, but with the row and column, indices swapped.

B[i][j] = A[j][i]

C Program to Find the Transpose of a Square Matrix

The below program finds the transpose of A[][] and stores the result in B[][], we can change N for different dimensions.

C

// C Program to find transpose
// of a square matrix
#include <stdio.h>
#define N 4

// This function stores transpose
// of A[][] in B[][]
void transpose(int A[][N], int B[][N])
{
    int i, j;
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            // Assigns the transpose of element A[j][i] to
            // B[i][j]
            B[i][j] = A[j][i];
}

// Driver code
int main()
{
    int A[N][N] = { { 1, 1, 1, 1 },
                    { 2, 2, 2, 2 },
                    { 3, 3, 3, 3 },
                    { 4, 4, 4, 4 } };

    int B[N][N], i, j;

    transpose(A, B);

    printf("Result matrix is \n");
    for (i = 0; i < N; i++) {
        for (j = 0; j < N; j++)
            printf("%d ", B[i][j]);
        printf("\n");
    }

    return 0;
}

Output

Result matrix is 
1 2 3 4 
1 2 3 4 
1 2 3 4 
1 2 3 4 

Complexity Analysis

• Time Complexity: O(n²)
• Auxiliary Space: O(n ²)

C Program to find Transpose of a Rectangular Matrix

The below program finds the transpose of A[][] and stores the result in B[][].

C

// C program to find transpose
// of a rectangular matrix
#include <stdio.h>
#define M 3
#define N 4

// This function stores transpose
// of A[][] in B[][]
void transpose(int A[][N], int B[][M])
{
    int i, j;
    for (i = 0; i < N; i++)
        for (j = 0; j < M; j++)
            B[i][j] = A[j][i];
}

// Driver code
int main()
{
    int A[M][N] = { { 1, 1, 1, 1 },
                    { 2, 2, 2, 2 },
                    { 3, 3, 3, 3 } };

    // Note dimensions of B[][]
    int B[N][M], i, j;

    transpose(A, B);

    printf("Result matrix is \n");
    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++)
            printf("%d ", B[i][j]);
        printf("\n");
    }

    return 0;
}

Output

Result matrix is 
1 2 3 
1 2 3 
1 2 3 
1 2 3 

Complexity Analysis

• Time Complexity: O(n*m)
• Auxiliary Space: O(n*m)

Please refer complete article on Program to find the transpose of a matrix for more details!