Given two matrices, the task is to multiply them. Matrices can either be square or rectangular:
Examples:
(Square Matrix Multiplication)
Input: mat1[m][n] = { {1, 1}, {2, 2} }
mat2[n][p] = { {1, 1}, {2, 2} }
Output: result[m][p] = { {3, 3}, {6, 6} }
(Rectangular Matrix Multiplication)
Input: mat1[3][2] = { {1, 1}, {2, 2}, {3, 3} }
mat2[2][3] = { {1, 1, 1}, {2, 2, 2} }
Output: result[3][3] = { {3, 3, 3}, {6, 6, 6}, {9, 9, 9} }
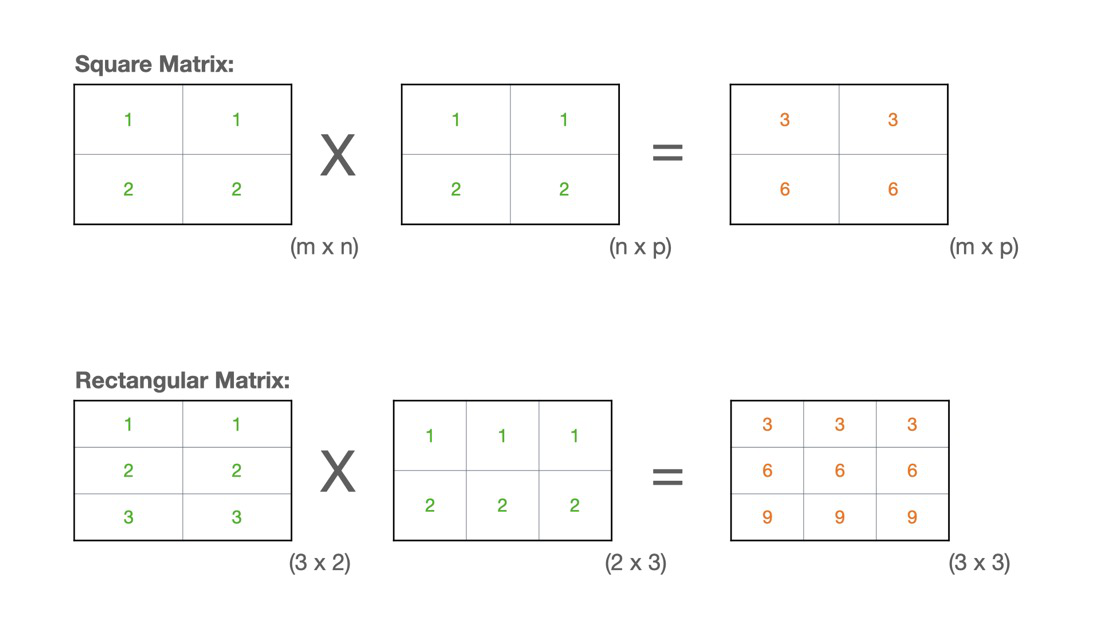
Multiplication of two Square or Rectangular Matrices:
- The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2.
- Output of multiplication of Matrix-1 and Matrix-2, results with equal to the number of rows of Matrix-1 and the number of columns of Matrix-2 i.e. rslt[R1][C2]
Below is the implementation of the multiplication of two matrices:
C
#include <stdio.h>
#include <stdlib.h>
#define R1 2 // number of rows in Matrix-1
#define C1 2 // number of columns in Matrix-1
#define R2 2 // number of rows in Matrix-2
#define C2 2 // number of columns in Matrix-2
void mulMat(int mat1[][C1], int mat2[][C2])
{
int rslt[R1][C2];
printf("Multiplication of given two matrices is:\n");
for (int i = 0; i < R1; i++) {
for (int j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (int k = 0; k < R2; k++) {
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
printf("%d\t", rslt[i][j]);
}
printf("\n");
}
}
int main()
{
int mat1[R1][C1] = { { 1, 1 },
{ 2, 2 } };
int mat2[R2][C2] = { { 1, 1 },
{ 2, 2 } };
if (C1 != R2) {
printf("The number of columns in Matrix-1 must be "
"equal to the number of rows in "
"Matrix-2\n");
printf("Please update MACROs value according to "
"your array dimension in "
"#define section\n");
exit(EXIT_FAILURE);
}
mulMat(mat1, mat2);
return 0;
}
|
C++
#include <bits/stdc++.h>
using namespace std;
#define R1 2 // number of rows in Matrix-1
#define C1 2 // number of columns in Matrix-1
#define R2 2 // number of rows in Matrix-2
#define C2 2 // number of columns in Matrix-2
void mulMat(int mat1[][C1], int mat2[][C2])
{
int rslt[R1][C2];
cout << "Multiplication of given two matrices is:\n";
for (int i = 0; i < R1; i++) {
for (int j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (int k = 0; k < R2; k++) {
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
cout << rslt[i][j] << "\t";
}
cout << endl;
}
}
int main()
{
int mat1[R1][C1] = { { 1, 1 },
{ 2, 2 } };
int mat2[R2][C2] = { { 1, 1 },
{ 2, 2 } };
if (C1 != R2) {
cout << "The number of columns in Matrix-1 must "
"be equal to the number of rows in "
"Matrix-2"
<< endl;
cout << "Please update MACROs according to your "
"array dimension in #define section"
<< endl;
exit(EXIT_FAILURE);
}
mulMat(mat1, mat2);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int R1 = 2;
static int C1 = 2;
static int R2 = 2;
static int C2 = 2;
static void mulMat(int[][] mat1, int[][] mat2)
{
int[][] rslt = new int[R1][C2];
System.out.println(
"Multiplication of given two matrices is:");
int i, j, k;
for (i = 0; i < R1; i++) {
for (j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (k = 0; k < R2; k++)
rslt[i][j] += mat1[i][k] * mat2[k][j];
System.out.print(rslt[i][j] + " ");
}
System.out.println("");
}
}
public static void main(String[] args)
{
int[][] mat1 = { { 1, 1 },
{ 2, 2 } };
int[][] mat2 = { { 1, 1 },
{ 2, 2 } };
if (C1 != R2) {
System.out.println(
"The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
System.out.println(
"Please update the global variables according to your array dimension");
}
else {
mulMat(mat1, mat2);
}
}
}
|
Python3
def mulMat(mat1, mat2, R1, R2, C1, C2):
rslt = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
for i in range(0, R1):
for j in range(0, C2):
for k in range(0, R2):
rslt[i][j] += mat1[i][k] * mat2[k][j]
print("Multiplication of given two matrices is:")
for i in range(0, R1):
for j in range(0, C2):
print(rslt[i][j], end=" ")
print("\n", end="")
if __name__ == '__main__':
R1 = 2
R2 = 2
C1 = 2
C2 = 2
mat1 = [[1, 1],
[2, 2]]
mat2 = [[1, 1],
[2, 2]]
if C1 != R2:
print("The number of columns in Matrix-1 must be equal to the number of rows in " + "Matrix-2", end='')
print("\n", end='')
print("Please update MACROs according to your array dimension in #define section", end='')
print("\n", end='')
else:
mulMat(mat1, mat2, R1, R2, C1, C2)
|
C#
using System;
class GFG {
static int R1 = 2;
static int C1 = 2;
static int R2 = 2;
static int C2 = 2;
static void mulMat(int[, ] mat1, int[, ] mat2)
{
int[, ] rslt = new int[R1, C2];
Console.WriteLine(
"Multiplication of given two matrices is:");
int i, j, k;
for (i = 0; i < R1; i++) {
for (j = 0; j < C2; j++) {
rslt[i, j] = 0;
for (k = 0; k < R2; k++)
rslt[i, j] += mat1[i, k] * mat2[k, j];
Console.Write(rslt[i, j] + "\t");
}
Console.WriteLine();
}
}
public static void Main()
{
int[, ] mat1 = { { 1, 1 },
{ 2, 2 } };
int[, ] mat2 = { { 1, 1 },
{ 2, 2 } };
if (C1 != R2) {
Console.WriteLine(
"The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
Console.WriteLine(
"Please update MACROs according to your array dimension in #define section");
}
else {
mulMat(mat1, mat2);
}
}
}
|
Javascript
var R1 = 2;
var C1 = 2;
var R2 = 2;
var C2 = 2;
function mulMat(mat1, mat2)
{
var rslt = Array(R1).fill(0).map(()=>new Array(C2).fill(0));
console.log("Multiplication of given two matrices is:");
var i = 0;
var j = 0;
var k = 0;
for (i = 0; i < R1; i++)
{
for (j = 0; j < C2; j++)
{
rslt[i][j] = 0;
for (k = 0; k < R2; k++)
{
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
console.log(rslt[i][j] + " ");
}
console.log("");
}
}
var mat1 = [[1, 1], [2, 2]];
var mat2 = [[1, 1], [2, 2]];
if (C1 != R2)
{
console.log("The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
console.log("Please update the global variables according to your array dimension");
}
else
{
mulMat(mat1, mat2);
}
|
OutputMultiplication of given two matrices is:
3 3
6 6
Time complexity: O(R1 * C2 * R2) for given matrices mat1[R1][C1] and mat2[R2][C2]
Auxiliary space: O(R1 * C2)
Multiplication of Rectangular Matrices using Pointers in C/C++:
To solve the problem follow the below idea:
We use pointers in C/C++ to multiply matrices
Prerequisite: How to pass a 2D array as a parameter in C?
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void multiply(int m1, int m2, int mat1[][2], int n1, int n2,
int mat2[][2])
{
int x, i, j;
int res[m1][n2];
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
res[i][j] = 0;
for (x = 0; x < m2; x++) {
*(*(res + i) + j) += *(*(mat1 + i) + x)
* *(*(mat2 + x) + j);
}
}
}
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
cout << *(*(res + i) + j) << " ";
}
cout << "\n";
}
}
int main()
{
int mat1[][2] = { { 1, 1 }, { 2, 2 } };
int mat2[][2] = { { 1, 1 }, { 2, 2 } };
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
multiply(m1, m2, mat1, n1, n2, mat2);
return 0;
}
|
C
#include <stdio.h>
void multiply(int m1, int m2, int mat1[][m2], int n1,
int n2, int mat2[][n2])
{
int x, i, j;
int res[m1][n2];
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
res[i][j] = 0;
for (x = 0; x < m2; x++) {
*(*(res + i) + j) += *(*(mat1 + i) + x)
* *(*(mat2 + x) + j);
}
}
}
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
printf("%d ", *(*(res + i) + j));
}
printf("\n");
}
}
int main()
{
int mat1[][2] = { { 1, 1 }, { 2, 2 } };
int mat2[][2] = { { 1, 1 }, { 2, 2 } };
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
multiply(m1, m2, mat1, n1, n2, mat2);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
public class GFG {
public static void multiply(int m1, int m2,
int mat1[][], int n1,
int n2, int mat2[][])
{
int x, i, j;
int res[][] = new int[m1][n2];
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
res[i][j] = 0;
for (x = 0; x < m2; x++) {
res[i][j] += mat1[i][x] * mat2[x][j];
}
}
}
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
System.out.print(res[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args)
{
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
int mat1[][] = new int[][] { { 1, 1 }, { 2, 2 } };
int mat2[][] = new int[][] { { 1, 1 }, { 2, 2 } };
multiply(m1, m2, mat1, n1, n2, mat2);
}
}
|
Python3
def multiply(m1, m2, mat1, n1, n2, mat2):
res = [[0 for x in range(n2)] for y in range(m1)]
for i in range(m1):
for j in range(n2):
res[i][j] = 0
for x in range(m2):
res[i][j] += mat1[i][x] * mat2[x][j]
for i in range(m1):
for j in range(n2):
print(res[i][j], end=" ")
print()
m1 = 2
m2 = 2
n1 = 2
n2 = 2
mat1 = [[1, 1], [2, 2]]
mat2 = [[1, 1], [2, 2]]
multiply(m1, m2, mat1, n1, n2, mat2)
|
C#
using System;
class Program {
static void Main(string[] args)
{
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
int[, ] mat1 = new int[, ] { { 1, 1 }, { 2, 2 } };
int[, ] mat2 = new int[, ] { { 1, 1 }, { 2, 2 } };
multiply(m1, m2, mat1, n1, n2, mat2);
}
static void multiply(int m1, int m2, int[, ] mat1,
int n1, int n2, int[, ] mat2)
{
int x, i, j;
int[, ] res = new int[m1, n2];
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
res[i, j] = 0;
for (x = 0; x < m2; x++) {
res[i, j] += mat1[i, x] * mat2[x, j];
}
}
}
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
Console.Write(res[i, j] + " ");
}
Console.WriteLine();
}
}
}
|
Javascript
function multiply(m1, m2, mat1, n1, n2, mat2) {
let x, i, j;
let res = [[0, 0], [0, 0]];
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
for (x = 0; x < m2; x++) {
res[i][j] += (mat1[i][x] * mat2[x][j])
}
}
}
for (i = 0; i < m1; i++) {
for (j = 0; j < n2; j++) {
console.log(res[i][j]);
}
}
}
let mat1 = [[1, 1], [2, 2]];
let mat2 = [[1, 1], [2, 2]];
let m1 = 2, m2 = 2, n1 = 2, n2 = 2;
multiply(m1, m2, mat1, n1, n2, mat2);
|
Time complexity: O(N3)
Auxiliary Space: O(M1 * N2)
Related Article: Strassen’s Matrix Multiplication
This article is contributed by Aditya Ranjan. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.