C program for Time Complexity plot of Bubble, Insertion and Selection Sort using Gnuplot
Last Updated :
24 Nov, 2021
Prerequisite:Comparison among bubble sort, insertion sort and selection sort.
Write a C program to plot and analyze the time complexity of Bubble sort, Insertion sort and Selection sort (using Gnuplot).
As per the problem we have to plot a time complexity graph by just using C. So we will be making sorting algorithms as functions and all the algorithms are given to sort exactly the same array to keep the comparison fair.
Examples:
Input: randomly generated arrays (using rand() function)
of different sizes as input for sorting.
Output:
A_size, Bubble, Insertion, Selection
10000, 366263, 80736, 152975
20000, 1594932, 332101, 609388
30000, 3773121, 785790, 1441547
40000, 7174455, 1574855, 2620006
50000, 10917061, 2029586, 4025993
60000, 15484338, 2998403, 5556494
70000, 21201561, 4146680, 7678139
80000, 29506758, 6027335, 10131950
90000, 36457272, 6699452, 12436376
100000, 43472313, 8335881, 15208712
Approach: We will be using arrays of different sizes to plot the graph between the time taken by the sorting algorithm versus array size. Execution of the program will take some time for sorting arrays of size up to 100000 elements.
Below is the implementation of the above approach:
// C program to store time taken by bubble sort,
// insertion sort and selection sort
// for sorting exactly same arrays.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Swap utility
void swap(long int* a, long int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// Bubble sort
void bubbleSort(long int a[], long int n)
{
for (long int i = 0; i < n - 1; i++) {
for (long int j = 0; j < n - 1 - i; j++) {
if (a[j] > a[j + 1]) {
swap(&a[j], &a[j + 1]);
}
}
}
}
// Insertion sort
void insertionSort(long int arr[], long int n)
{
long int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// Move elements of arr[0..i-1], that are
// greater than key, to one position ahead
// of their current position
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// Selection sort
void selectionSort(long int arr[], long int n)
{
long int i, j, midx;
for (i = 0; i < n - 1; i++) {
// Find the minimum element in unsorted array
midx = i;
for (j = i + 1; j < n; j++)
if (arr[j] < arr[min_idx])
midx = j;
// Swap the found minimum element
// with the first element
swap(&arr[midx], &arr[i]);
}
}
// Driver code
int main()
{
long int n = 10000;
int it = 0;
// Arrays to store time duration
// of sorting algorithms
double tim1[10], tim2[10], tim3[10];
printf("A_size, Bubble, Insertion, Selection\n");
// Performs 10 iterations
while (it++ < 10) {
long int a[n], b[n], c[n];
// generating n random numbers
// storing them in arrays a, b, c
for (int i = 0; i < n; i++) {
long int no = rand() % n + 1;
a[i] = no;
b[i] = no;
c[i] = no;
}
// using clock_t to store time
clock_t start, end;
// Bubble sort
start = clock();
bubbleSort(a, n);
end = clock();
tim1[it] = ((double)(end - start));
// Insertion sort
start = clock();
insertionSort(b, n);
end = clock();
tim2[it] = ((double)(end - start));
// Selection sort
start = clock();
selectionSort(c, n);
end = clock();
tim3[it] = ((double)(end - start));
// type conversion to long int
// for plotting graph with integer values
printf("%li, %li, %li, %li\n",
n,
(long int)tim1[it],
(long int)tim2[it],
(long int)tim3[it]);
// increases the size of array by 10000
n += 10000;
}
return 0;
}
|
Output:
A_size, Bubble, Insertion, Selection
10000, 366263, 80736, 152975
20000, 1594932, 332101, 609388
30000, 3773121, 785790, 1441547
40000, 7174455, 1574855, 2620006
50000, 10917061, 2029586, 4025993
60000, 15484338, 2998403, 5556494
70000, 21201561, 4146680, 7678139
80000, 29506758, 6027335, 10131950
90000, 36457272, 6699452, 12436376
100000, 43472313, 8335881, 15208712
Now comes the question that how are we going to plot a graph on x-y coordinates?
For that, we will be using a very simple utility called Gnuplot.
Gnuplot is a portable command-line driven graphing utility for Linux, MS Windows, OSX and many other platforms.
Note:In this article, Ubuntu(Linux) is used.
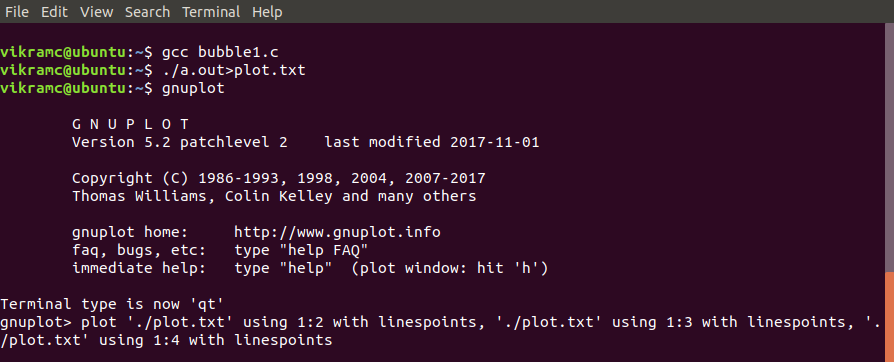
- First things first how to install Gnuplot.Use this command to install Gnuplot.
sudo apt-get install gnuplot
- After this compile your code and copy the output in a text file using this command.
./a.out>plot.txt
- Open Gnuplot simply using.
gnuplot
- Now the last thing is to plot the graph so use this command to plot the complexity graph.
plot './plot.txt' using 1:2 with linespoints,
'./plot.txt' using 1:3 with linespoints,
'./plot.txt' using 1:4 with linespoints
Here is a terminal-snap of commands.
Here is the graph of complexity comparing bubble sort(purple curve), insertion sort(green curve) and selection sort(blue curve).

Observation:
The average time complexity of all three algorithms is O(n^2) but as the size of input data increases, insertion sort performs far better than bubble sort and slightly better than selection sort.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...