C Program for Legendre’s Conjecture

It says that there is always one prime number between any two consecutive natural number’s(n = 1, 2, 3, 4, 5, …) square. This is called Legendre’s Conjecture. Conjecture: A conjecture is a proposition or conclusion based upon incomplete information to which no proof has been found i.e it has not been proved or disproved.

Mathematically, there is always one prime p in the range 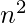to 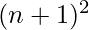where n is any natural number. for examples- 2 and 3 are the primes in the range 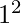to 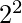. 5 and 7 are the primes in the range 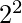to 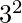. 11 and 13 are the primes in the range 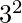to 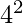. 17 and 19 are the primes in the range 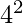to .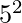

Examples:

Input : 4 
output: Primes in the range 16 and 25 are:
        17
        19
        23

Explanation: Here 4² = 16 and 5² = 25 Hence, prime numbers between 16 and 25 are 17, 19 and 23.

Input : 10
Output: Primes in the range 100 and 121 are:
        101
        103
        107
        109
        113

CPP

// CPP program to verify Legendre's Conjecture
// for a given n.
#include <bits/stdc++.h>
using namespace std;

// prime checking
bool isprime(int n)
{
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
            return false;
    return true;
}

void LegendreConjecture(int n)
{
    cout << "Primes in the range " << n * n
        << " and " << (n + 1) * (n + 1)
        << " are:" << endl;

    for (int i = n * n; i <= ((n + 1) * (n + 1)); i++)

        // searching for primes
        if (isprime(i))
            cout << i << endl;
}

// Driver program
int main()
{
    int n = 50;
    LegendreConjecture(n);
    return 0;
}

Output:

Primes in the range 2500 and 2601 are:
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593

Time Complexity: O(n²). isPrime() function takes O(n) time and it is embedded in LegendreConjecture() function which also takes O(n) time as it has loop which starts from n² and ends at 
(n+1)²   so,  (n+1)² – n² = 2n+1.

Auxiliary Space: O(1)

Please refer complete article on Legendre’s Conjecture for more details!