C Program for Legendre’s Conjecture
Last Updated :
16 Nov, 2022
It says that there is always one prime number between any two consecutive natural number’s(n = 1, 2, 3, 4, 5, …) square. This is called Legendre’s Conjecture. Conjecture: A conjecture is a proposition or conclusion based upon incomplete information to which no proof has been found i.e it has not been proved or disproved.
Mathematically, there is always one prime p in the range 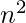 to
to 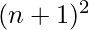 where n is any natural number. for examples- 2 and 3 are the primes in the range
where n is any natural number. for examples- 2 and 3 are the primes in the range 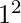 to
to 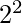 . 5 and 7 are the primes in the range
. 5 and 7 are the primes in the range 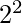 to
to 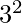 . 11 and 13 are the primes in the range
. 11 and 13 are the primes in the range 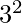 to
to 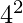 . 17 and 19 are the primes in the range
. 17 and 19 are the primes in the range 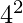 to
to 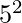 .
.
Examples:
Input : 4
output: Primes in the range 16 and 25 are:
17
19
23
Explanation: Here 42 = 16 and 52 = 25 Hence, prime numbers between 16 and 25 are 17, 19 and 23.
Input : 10
Output: Primes in the range 100 and 121 are:
101
103
107
109
113
CPP
#include <bits/stdc++.h>
using namespace std;
bool isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
void LegendreConjecture(int n)
{
cout << "Primes in the range " << n * n
<< " and " << (n + 1) * (n + 1)
<< " are:" << endl;
for (int i = n * n; i <= ((n + 1) * (n + 1)); i++)
if (isprime(i))
cout << i << endl;
}
int main()
{
int n = 50;
LegendreConjecture(n);
return 0;
}
|
Output:Primes in the range 2500 and 2601 are:
2503
2521
2531
2539
2543
2549
2551
2557
2579
2591
2593
Time Complexity: O(n2). isPrime() function takes O(n) time and it is embedded in LegendreConjecture() function which also takes O(n) time as it has loop which starts from n2 and ends at
(n+1)2 so, (n+1)2 – n2 = 2n+1.
Auxiliary Space: O(1)
Please refer complete article on Legendre’s Conjecture for more details!
Share your thoughts in the comments
Please Login to comment...