C Program for Kronecker Product of two matrices
Last Updated :
23 Apr, 2022
Given a 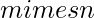 matrix A and a
matrix A and a 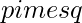 matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an
matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an 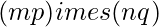 matrix.
matrix.
A tensor B = |a11B a12B|
|a21B a22B|
= |a11b11 a11b12 a12b11 a12b12|
|a11b21 a11b22 a12b21 a12b22|
|a11b31 a11b32 a12b31 a12b32|
|a21b11 a21b12 a22b11 a22b12|
|a21b21 a21b22 a22b21 a22b22|
|a21b31 a21b32 a22b31 a22b32|
Examples:
1. The matrix direct(kronecker) product of the 2×2 matrix A
and the 2×2 matrix B is given by the 4×4 matrix :
Input : A = 1 2 B = 0 5
3 4 6 7
Output : C = 0 5 0 10
6 7 12 14
0 15 0 20
18 21 24 28
2. The matrix direct(kronecker) product of the 2×3 matrix A
and the 3×2 matrix B is given by the 6×6 matrix :
Input : A = 1 2 B = 0 5 2
3 4 6 7 3
1 0
Output : C = 0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Below is the code to find the Kronecker Product of two matrices and stores it as matrix C :
C
#include <stdio.h>
const int cola = 2, rowa = 3, colb = 3, rowb = 2;
void Kroneckerproduct(int A[][cola], int B[][colb])
{
int C[rowa * rowb][cola * colb];
for (int i = 0; i < rowa; i++) {
for (int k = 0; k < rowb; k++) {
for (int j = 0; j < cola; j++) {
for (int l = 0; l < colb; l++) {
C[i + l + 1][j + k + 1] = A[i][j] * B[k][l];
printf("%d ", C[i + l + 1][j + k + 1]);
}
}
printf("
");
}
}
}
int main()
{
int A[3][2] = { { 1, 2 }, { 3, 4 }, { 1, 0 } },
B[2][3] = { { 0, 5, 2 }, { 6, 7, 3 } };
Kroneckerproduct(A, B);
return 0;
}
|
Output :
0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Time Complexity: O(rowa*cola*rowb*colb), as we are using nested loops.
Auxiliary Space: O(rowa*cola*rowb*colb), as we are using extra space in the matrix C.
Please refer complete article on Kronecker Product of two matrices for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...