C Program for Find largest prime factor of a number
Last Updated :
25 Apr, 2023
Given a positive integer ‘n'( 1 <= n <= 1015). Find the largest prime factor of a number.
Input: 6
Output: 3
Explanation
Prime factor of 6 are- 2, 3
Largest of them is '3'
Input: 15
Output: 5
Method 1:
The approach is simple, just factorise the given number by dividing it with the divisor of a number and keep updating the maximum prime factor. See this to understand more.
c
#include <math.h>
long long maxPrimeFactors(long long n)
{
long long maxPrime = -1;
while (n % 2 == 0) {
maxPrime = 2;
n >>= 1;
}
for (int i = 3; i * i <= n; i += 2) {
while (n % i == 0) {
maxPrime = i;
n = n / i;
}
}
if (n > 2)
maxPrime = n;
return maxPrime;
}
int main()
{
long long n = 15;
printf("%lld\n", maxPrimeFactors(n));
n = 25698751364526;
printf("%lld", maxPrimeFactors(n));
return 0;
}
|
Time complexity: 
Auxiliary space: 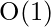
Method 2:
Follow the steps below for the implementation:
- Initialize variables largest_prime to -1, i to 2, and n to the input integer.
- Start a while loop that continues as long as i * i <= n. This loop will iterate through all possible factors of n.
- In the while loop, start another while loop that continues as long as n % i == 0. This inner loop will divide n by i until n is no longer divisible by i.
- In the inner loop, set largest_prime to i, and update n by dividing it by i.
- At the end of the inner loop, increment i by 1.
- After the outer loop, if n > 1, set largest_prime to n. This is because n could be a prime number larger than any of its factors.
- Return largest_prime.
Below is the implementation of the above approach:
C
#include <stdio.h>
long long maxPrimeFactors(long long n)
{
long long largest_prime = -1, i = 2;
while (i * i <= n) {
while (n % i == 0) {
largest_prime = i;
n = n / i;
}
i = i + 1;
}
if (n > 1) {
largest_prime = n;
}
return largest_prime;
}
int main()
{
long long n = 15;
printf("%lld\n", maxPrimeFactors(n));
n = 25698751364526;
printf("%lld\n", maxPrimeFactors(n));
return 0;
}
|
Time complexity: O(sqrt(n)).
Auxiliary space: O(1)
Please refer complete article on Find largest prime factor of a number for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...