Build a DFA to accept a binary string containing “01” i times and “1” 2j times
Last Updated :
30 Mar, 2023
Given a binary string str, the task is to build a DFA that accepts given binary string if it contains “01” i times and “1” 2j times, i.e.,
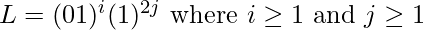
Examples:
Input: str = “011111”
Output: Accepted
Explanation:
The string follows the language as: (01)1(1)2*2
Input: str = “01111”
Output: Not Accepted
DFA or Deterministic Finite Automata is a finite state machine which accepts a string(under some specific condition) if it reaches a final state, otherwise rejects it.
In DFA, there is no concept of memory, therefore we have to check the string character by character, beginning with the 0th character. The input set of characters for the problem is {0, 1}. For a DFA to be valid, there must a transition rule defined for each symbol of the input set at every state to a valid state. Therefore, the following steps are followed to design the DFA:
- Create initial stage and make the transition of 0 and 1 to next possible state.
- Transition of 0 is always followed by transition of 1.
- Make an initial state and transit its input alphabets, i.e, 0 and 1 to two different states.
- Check for acceptance of string after each transition to ignore errors.
- First, make DfA for minimum length string then go ahead step by step.
- Define Final State(s) according to the acceptance of string.
Step by Step Approach to design a DFA:
- Step 1: Minimum possible acceptable string is 0111, i.e, (01)1 (11)1. So, create an initial state “A” that make transition of 0 to state “B” and then transition of 1 from “B” to state “C” then transition of 1 from “C” to “D”, then transition of 1 from “D” to “E” as shown in diagram make this stage “E” is final state.

- Step 2: Now, think about the string having consecutive (01) and then followed by consecutive (11) to end the string. Hence, when i>1, make a transition of “0” from state “C” to state “B” and make a transition of “1” from the state “E” to state “D”. Hence, strings like 010111, 011111, 0101111111, etc. are acceptable now.
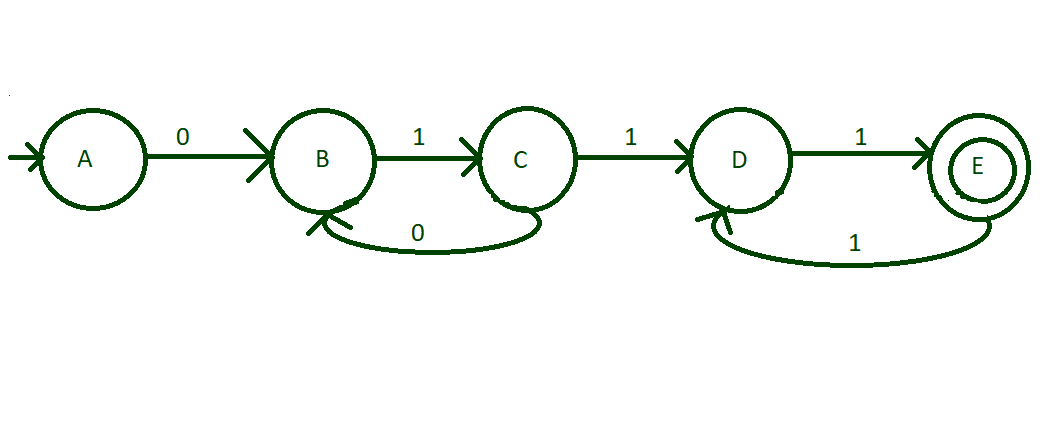
- Step 3: We have done with all kind of strings possible to accept. But, there are few input alphabets which are not transited to any of the states. In this case, all these kind of input will be sent to some dead state to block their further transitions that are not acceptable. Input alphabets of the dead state will be sent to the dead state itself. Therefore, the final design of the DFA is:

Below is the implementation of the above approach:
C++
#include <iostream>
#include <string>
using namespace std;
void checkstatea(string n);
void stateb(string n);
void statec(string n);
void stated(string n);
void statee(string n);
int main() {
string n = "011111";
checkstatea(n);
return 0;
}
void checkstatea(string n) {
if (n.length() % 2 != 0 || n.length() < 4) {
cout << "string not accepted" << endl;
} else {
int i = 0;
if (n[i] == '0') {
stateb(n.substr(1));
} else {
cout << "string not accepted" << endl;
}
}
}
void stateb(string n) {
int i = 0;
if (n[i] == '0') {
cout << "string not accepted" << endl;
} else {
statec(n.substr(1));
}
}
void statec(string n) {
int i = 0;
if (n[i] == '1') {
stated(n.substr(1));
} else {
stateb(n.substr(1));
}
}
void stated(string n) {
int i = 0;
if (n.length() == 1) {
if (n[i] == '1') {
cout << "string accepted" << endl;
} else {
cout << "string not accepted" << endl;
}
} else {
if (n[i] == '1') {
statee(n.substr(1));
} else {
cout << "string not accepted" << endl;
}
}
}
void statee(string n) {
int i = 0;
if (n.length() == 1) {
if (n[i] == '0') {
cout << "string not accepted" << endl;
} else {
cout << "string accepted" << endl;
}
} else {
if (n[i] == '0') {
cout << "string not accepted" << endl;
} else {
stated(n.substr(1));
}
}
}
|
Java
import java.util.*;
class GFG{
static void checkstatea(String n)
{
if (n.length() % 2 != 0 ||
n.length() < 4)
System.out.print("string not accepted");
else
{
int i = 0;
if (n.charAt(i) == '0')
stateb(n.substring(1));
else
System.out.print("string not accepted");
}
}
static void stateb(String n)
{
int i = 0;
if (n.charAt(i) == '0')
System.out.print("string not accepted");
else
statec(n.substring(1));
}
static void statec(String n)
{
int i = 0;
if (n.charAt(i) == '1')
stated(n.substring(1));
else
stateb(n.substring(1));
}
static void stated(String n)
{
int i = 0;
if (n.length() == 1)
{
if (n.charAt(i) == '1')
System.out.print("string accepted");
else
System.out.print("string not accepted");
}
else
{
if (n.charAt(i) == '1')
statee(n.substring(1));
else
System.out.print("string not accepted");
}
}
static void statee(String n)
{
int i = 0;
if (n.length() == 1)
{
if (n.charAt(i) == '0')
System.out.print("string not accepted");
else
System.out.print("string accepted");
}
else
{
if (n.charAt(i) == '0')
System.out.print("string not accepted");
stated(n.substring(1));
}
}
public static void main(String []args)
{
String n ="011111";
checkstatea(n);
}
}
|
Python3
def checkstatea(n):
if(len(n)%2!=0 or len(n)<4):
print("string not accepted")
else:
i=0
if(n[i]=='0'):
stateb(n[1:])
else:
print("string not accepted")
def stateb(n):
i=0
if(n[i]=='0'):
print("string not accepted")
else:
statec(n[1:])
def statec(n):
i=0
if(n[i]=='1'):
stated(n[1:])
else:
stateb(n[1:])
def stated(n):
i=0
if(len(n)==1):
if(n[i]=='1'):
print("string accepted")
else:
print("string not accepted")
else:
if(n[i]=='1'):
statee(n[1:])
else:
print("string not accepted")
def statee(n):
i=0
if(len(n)==1):
if(n[i]=='0'):
print("string not accepted")
else:
print("string accepted")
else:
if(n[i]=='0'):
print("string not accepted")
stated(n[1:])
if __name__ == "__main__":
n = "011111"
checkstatea(n)
|
Javascript
<script>
function checkstatea(n) {
if (n.length % 2 !== 0 || n.length < 4)
document.write("string not accepted");
else {
var i = 0;
if (n[i] === "0") stateb(n.substring(1));
else document.write("string not accepted");
}
}
function stateb(n) {
var i = 0;
if (n[i] === "0") document.write("string not accepted");
else statec(n.substring(1));
}
function statec(n) {
var i = 0;
if (n[i] === "1") stated(n.substring(1));
else stateb(n.substring(1));
}
function stated(n) {
var i = 0;
if (n.length === 1) {
if (n[i] === "1") document.write("string accepted");
else document.write("string not accepted");
} else {
if (n[i] === "1") statee(n.substring(1));
else document.write("string not accepted");
}
}
function statee(n) {
var i = 0;
if (n.length == 1) {
if (n[i] === "0") document.write("string not accepted");
else document.write("string accepted");
} else {
if (n[i] === "0") document.write("string not accepted");
stated(n.substring(1));
}
}
var n = "011111";
checkstatea(n);
</script>
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
static void checkstatea(string n)
{
if(n.Length % 2 != 0 ||
n.Length < 4)
Console.Write("string not accepted");
else
{
int i = 0;
if(n[i] == '0')
stateb(n.Substring(1));
else
Console.Write("string not accepted");
}
}
static void stateb(string n)
{
int i = 0;
if(n[i] == '0')
Console.Write("string not accepted");
else
statec(n.Substring(1));
}
static void statec(string n)
{
int i = 0;
if(n[i] == '1')
stated(n.Substring(1));
else
stateb(n.Substring(1));
}
static void stated(string n)
{
int i = 0;
if(n.Length == 1)
{
if(n[i] == '1')
Console.Write("string accepted");
else
Console.Write("string not accepted");
}
else
{
if(n[i] == '1')
statee(n.Substring(1));
else
Console.Write("string not accepted");
}
}
static void statee(string n)
{
int i = 0;
if(n.Length == 1)
{
if(n[i] == '0')
Console.Write("string not accepted");
else
Console.Write("string accepted");
}
else
{
if(n[i] == '0')
Console.Write("string not accepted");
stated(n.Substring(1));
}
}
public static void Main(string []args)
{
string n ="011111";
checkstatea(n);
}
}
|
Time complexity: O(N) where N is length of string input
Auxiliary space: O(N)
Share your thoughts in the comments
Please Login to comment...