Breaking a number such that first part is integral division of second by a power of 10
Last Updated :
27 Jul, 2022
Given a very large number N, we need to count the total ways such that if we divide the number into two parts a and b, the first part a can be obtained by integral division of second b by some power p of 10 and p>=0. 1 <= No of digits in N <= 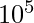 .
.
Examples:
Input : 220
Output : 1
220 can be divided as a = 2 and b = 20
such that for p = 1, b/10 = a.
Input : 1111
Output : 2
We get answer 2 because we need to consider
integral division.
Let's consider the first partition a = 1,
b = 111. for p = 2, b/pow(10,p) = a thus
this is a valid partition.
now a = 11, b = 11. for p = 0, b/pow(10,p)
= a thus this too is a valid combination.
Input : 2202200
Output : 2
for a = 2 b = 202200, p = 5 and
a = 220, b = 2200, p = 1
Since the number can be very large to be contained even in a long long int we will store it as a string. According to the conditions mentioned in the problem, division is the floor function. A simple and inefficient approach will be to divide the string into two substrings then convert those to integer and perform division. An efficient method to do it will be to use the string compare function to match the most significant digits of the two strings and ignore the rest( floor function).
Below is the implementation of this idea :
C++
#include <bits/stdc++.h>
using namespace std;
int calculate(string N)
{
int len = N.length();
int l = (len) / 2;
int count = 0;
for (int i = 1; i <= l; i++) {
string s = N.substr(0, i);
int l1 = s.length();
string t = N.substr(i, l1);
if (s[0] == '0' || t[0] == '0')
continue;
if (s.compare(t) == 0)
count++;
}
return count;
}
int main()
{
string N = "2202200";
cout << calculate(N);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int calculate(String N)
{
int len = N.length();
int l = (len) / 2;
int count = 0;
for (int i = 1; i <= l; i++)
{
String s = N.substring(0, i);
int l1 = s.length();
String t = N.substring(i, l1 + i);
if (s.charAt(0) == '0' || t.charAt(0) == '0')
continue;
if (s.compareTo(t) == 0)
count++;
}
return count;
}
public static void main(String[] args)
{
String N = "2202200";
System.out.print(calculate(N));
}
}
|
Python3
def calculate( N ):
length = len(N)
l = int((length) / 2)
count = 0
for i in range(l + 1):
print(i)
s = N[0: 0 + i]
l1 = len(s)
print(s,l1)
t = N[i: l1 + i]
try:
if s[0] == '0' or t[0] == '0':
continue
except:
continue
if s == t:
count+=1
print(i,N[i],count)
return count
N = str("2202200")
print(calculate(N))
|
C#
using System;
class GFG
{
static int calculate(String N)
{
int len = N.Length;
int l = (len) / 2;
int count = 0;
for (int i = 1; i <= l; i++)
{
String s = N.Substring(0, i);
int l1 = s.Length;
String t = N.Substring(i, l1);
if (s[0] == '0' || t[0] == '0')
continue;
if (s.CompareTo(t) == 0)
count++;
}
return count;
}
public static void Main(String[] args)
{
String N = "2202200";
Console.Write(calculate(N));
}
}
|
Javascript
<script>
function calculate( N ){
let len = N.length
let l = Math.floor((len) / 2)
let count = 0
for(let i = 1; i < l + 1; i++)
{
let s = N.substr(0, i)
let l1 = s.length
let t = N.substr(i,l1)
if (s[0] == '0' || t[0] == '0'){
continue
}
if(s === t)
count++
}
return count
}
let N = "2202200"
console.log(calculate(N))
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...