Boundary Value Analysis – Triangle Problem
Last Updated :
08 Feb, 2023
The triangle problem is a classic example of using boundary value analysis to test a software program. The problem involves determining if three values, representing the lengths of the sides of a triangle, form a valid triangle.
To perform boundary value analysis, we start by selecting test cases that include values at the boundaries of the input domain. In the case of the triangle problem, the input domain is defined by the length of each side, which can be any positive number.
The following are some example test cases for the triangle problem using boundary value analysis:
- The smallest possible triangle: 3 sides of length 1. This test case tests the lower boundary of the input domain.
- A degenerate triangle: 3 sides of length 0. This test case tests the case where the input values are at the lower boundary and are not valid.
- An equilateral triangle: 3 sides of equal length. This test case tests the case where all sides are equal.
- An isosceles triangle: 2 sides of equal length, the third side is different. This test case tests the case where two sides are equal.
- A scalene triangle: 3 sides of different length. This test case tests the case where all sides are different.
By testing these boundary values, we can ensure that the software program correctly handles the edge cases of the input domain and produces correct results for all possible inputs.
Boundary Value Analysis (BVA) is a black box software testing technique where test cases are designed using boundary values. BVA is based on the single fault assumption, also known as critical fault assumption which states that failures are rarely the product of two or more simultaneous faults. Hence while designing the test cases for BVA we keep all but one variable to the nominal value and allowing the remaining variable to take the extreme value.
Test Case Design for BVA: While designing the test cases for BVA first we determine the number of input variables in the problem. For each input variable, we then determine the range of values it can take. Then we determine the extreme values and nominal value for each input variable.
Consider an input variable t taking values in the range [l, r].Extreme values for t are –
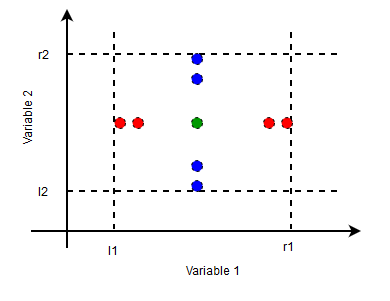
t = l
t = l+1
t = r-1
t = r
The nominal value for the variable can be any value in the range (l, r).
In most of the BVA implementations, it is taken as the middle value of the range (r+l)/2.
The figure on the right shows the nominal and extreme values for boundary value of analysis of a two variable problem.
Under the single fault assumption, the total number of test cases in BVA for a problem with n inputs is 4n+1.
The 4n cases correspond to the test cases with the four extreme values of each variable keeping the other n-1 variable at nominal value. The one additional case is where all variables are held at a nominal value.
One of the common problem for Test Case Design using BVA is the Triangle Problem that is discussed below –
Triangle Problem accepts three integers – a, b, c as three sides of the triangle .We also define a range for the sides of the triangle as [l, r] where l>0. It returns the type of triangle (Scalene, Isosceles, Equilateral, Not a Triangle) formed by a, b, c.
For a, b, c to form a triangle the following conditions should be satisfied –
a < b+c
b < a+c
c < a+b
If any of these conditions is violated output is Not a Triangle.
- For Equilateral Triangle all the sides are equal.
- For Isosceles Triangle exactly one pair of sides is equal.
- For Scalene Triangle all the sides are different.
The table shows the Test Cases Design for the Triangle Problem.The range value [l, r] is taken as [1, 100] and nominal value is taken as 50.
The total test cases is,
4n+1 = 4*3+1 = 13
| Test Case ID |
a |
b |
c |
Expected Output |
| T1 |
1 |
50 |
50 |
Isosceles |
| T2 |
2 |
50 |
50 |
Isosceles |
| T3 |
99 |
50 |
50 |
Isosceles |
| T4 |
100 |
50 |
50 |
Not a Triangle |
| T5 |
50 |
50 |
50 |
Equilateral |
| T6 |
50 |
1 |
50 |
Isosceles |
| T7 |
50 |
2 |
50 |
Isosceles |
| T8 |
50 |
99 |
50 |
Isosceles |
| T9 |
50 |
100 |
50 |
Not a Triangle |
| T10 |
50 |
50 |
1 |
Isosceles |
| T11 |
50 |
50 |
2 |
Isosceles |
| T12 |
50 |
50 |
99 |
Isosceles |
| T13 |
50 |
50 |
100 |
Not a Triangle |
Share your thoughts in the comments
Please Login to comment...