Bloom Filter in Java with Examples
Last Updated :
16 Apr, 2020
Bloom filters are for set membership which determines whether an element is present in a set or not. Bloom filter was invented by Burton H. Bloom in 1970 in a paper called Space/Time Trade-offs in Hash Coding with Allowable Errors (1970). Bloom filter is a probabilistic data structure that works on hash-coding methods (similar to HashTable).
When do we need a Bloom Filter?
Consider any of the following situations:
- Suppose we have a list of some elements and we want to check whether a given element is present or not?
- Consider you are working on email service and you are trying to implement sign up endpoint with a feature that a given username is already present or not?
- Suppose you have given a set of blacklisted IP’s and you want to filter out a given IP is a blacklisted one or not?
Can these problem be solved without the help of Bloom Filter?
Let us try to solve these problem using a HashSet
import java.util.HashSet;
import java.util.Set;
public class SetDemo {
public static void main(String[] args)
{
Set<String> blackListedIPs
= new HashSet<>();
blackListedIPs.add("192.170.0.1");
blackListedIPs.add("75.245.10.1");
blackListedIPs.add("10.125.22.20");
System.out.println(
blackListedIPs
.contains(
"75.245.10.1"));
System.out.println(
blackListedIPs
.contains(
"101.125.20.22"));
}
}
|
Why does data structure like HashSet or HashTable fail?
HashSet or HashTable works well when we have limited data set, but might not fit as we move with a large data set. With a large data set, it takes a lot of time with a lot of memory.
Size of Data set vs insertion time for HashSet like data structure
----------------------------------------------
|Number of UUIDs Insertion Time(ms) |
----------------------------------------------
|10 <1 |
|100 3 |
|1, 000 58 |
|10, 000 122 |
|100, 000 836 |
|1, 000, 000 7395 |
----------------------------------------------
Size of Data set vs memory (JVM Heap) for HashSet like data structure
----------------------------------------------
|Number of UUIDs JVM heap used(MB) |
----------------------------------------------
|10 <2 |
|100 <2 |
|1, 000 3 |
|10, 000 9 |
|100, 000 37 |
|1, 000, 000 264 |
-----------------------------------------------
So it is clear that if we have a large set of data then a normal data structure like the Set or HashTable is not feasible, and here Bloom filters come into the picture. Refer this article for more details on comparison between the two: Difference between Bloom filters and Hashtable
How to solve these problems with the help of Bloom Filter?
Let’s take a bit array of size N (Here 24) and initialize each bit with binary zero, Now take some hash functions (You can take as many you want, we are taking two hash function here for our illustration).

- Now pass the first IP you have to both hash function, which generates some random number as given below
hashFunction_1(192.170.0.1) : 2
hashFunction_2(192.170.0.1) : 6
Now, Go to index 2 and 6 and mark the bit as binary 1.

- Now pass the second IP you have, and follow the same step.
hashFunction_1(75.245.10.1) : 4
hashFunction_2(75.245.10.1) : 10
Now, Go to index 4 and 10 and mark the bit as binary 1.

- Similarly pass the third IP to the both hash function, and suppose you got the below output of hash function
hashFunction_1(10.125.22.20) : 10
hashFunction_2(10.125.22.20) : 19
‘
Now, go to index 10 and 19 and mark as binary 1, Here index 10 is already marked by previous entry so just mark the index 19 as binary 1.

Now, It is time to check whether an IP is present in the data set or not,
- Test input #1
Let’s say we want to check IP 75.245.10.1. Pass this IP with the same two hash functions which we have taken for adding the above inputs.
hashFunction_1(75.245.10.1) : 4
hashFunction_2(75.245.10.1) : 10
Now, Go to the index and check the bit, if both the index 4 and 10 is marked with binary 1 then the IP 75.245.10.1 is present in the set, otherwise it is not with the data set.
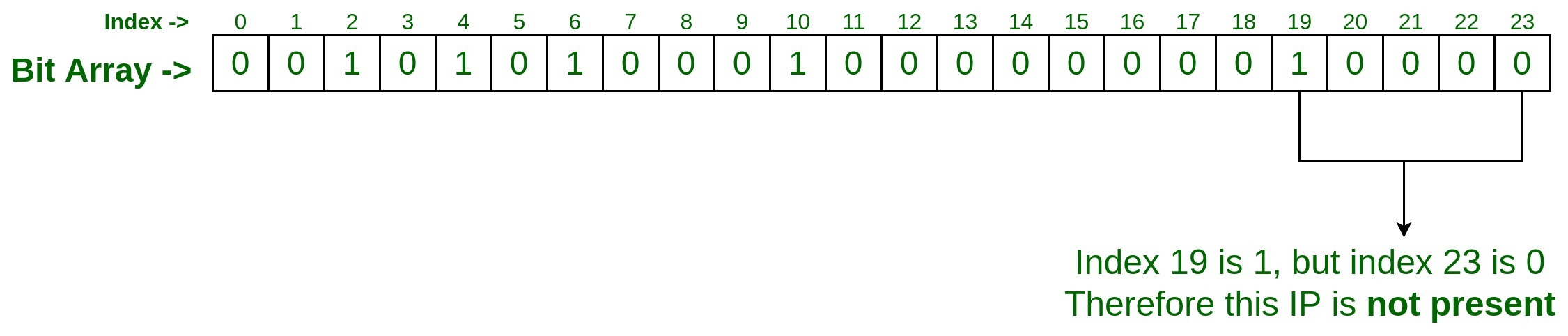
- Test input #2
Let’s say we want to check IP 75.245.20.30 is present in the set or not? So the process will be same, Pass this IP with the same two hash functions which we have taken for adding the above inputs.
hashFunction_1(75.245.20.30) : 19
hashFunction_2(75.245.20.30) : 23
Since at index 19 it is set to 1 but at index 23 it is 0, So we can say given IP 75.245.20.30 is not present in the set.

Why is Bloom Filter a probabilistic data structure?
Let’s understand this with one more test, This time consider an IP 101.125.20.22 and check whether it is present in the set or not. Pass this to both hash function. Consider our hash function results as follows.
hashFunction_1(101.125.20.22) : 19
hashFunction_2(101.125.20.22) : 2
Now, visit the index 19 and 2 which is set to 1 and it says that the given IP101.125.20.22 is present in the set.

But, this IP 101.125.20.22 has bot been processed above in the data set while adding the IP’s to bit array. This is known as False Positive:
Expected Output: No
Actual Output: Yes (False Positive)
In this case, index 2 and 19 were set to 1 by other input and not by this IP 101.125.20.22. This is called collision and that’s why it is probabilistic, where chances of happening are not 100%.
What to expect from a Bloom filter?
- When a Bloom filter says an element is not present it is for sure not present. It guarantees 100% that the given element is not available in the set, because either of the bit of index given by hash functions will be set to 0.
- But when Bloom filter says the given element is present it is not 100% sure, because there may be a chance due to collision all the bit of index given by hash functions has been set to 1 by other inputs.
How to get 100% accurate result from a Bloom filter?
Well, this could be achieved only by taking more number of hash functions. The more number of the hash function we take, the more accurate result we get, because of lesser chances of a collision.
Time and Space complexity of a Bloom filter
Suppose we have around 40 million data sets and we are using around H hash functions, then:
Time complexity: O(H), where H is the number of hash functions used
Space complexity: 159 Mb (For 40 million data sets)
Case of False positive: 1 mistake per 10 million (for H = 23)
Implementing Bloom filter in Java using Guava Library:
We can implement the Bloom filter using Java library provided by Guava.
- Include the below maven dependency:
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>19.0</version>
</dependency>
|
- Write the following code to implement the Bloom Filter:
import java.nio.charset.Charset;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
public class BloomFilterDemo {
public static void main(String[] args)
{
BloomFilter<String> blackListedIps
= BloomFilter.create(
Funnels.stringFunnel(
Charset.forName("UTF-8")),
10000);
blackListedIps.put("192.170.0.1");
blackListedIps.put("75.245.10.1");
blackListedIps.put("10.125.22.20");
System.out.println(
blackListedIps
.mightContain(
"75.245.10.1"));
System.out.println(
blackListedIps
.mightContain(
"101.125.20.22"));
}
}
|
Output:

Bloom Filter Output
Note: The above Java code may return a 3% false-positive probability by default.
- Reduce the false-positive probability
Introduce another parameter in Bloom filter object creation as follows:
BloomFilter blackListedIps = BloomFilter.create(Funnels.stringFunnel(Charset.forName("UTF-8")), 10000, 0.005);
Now false-positive probability has been reduced from 0.03 to 0.005. But tweaking this parameter has an effect on the side of the bloom filter.
Effect of reducing the false positive probability:
Let’s analyze this effect with respect to the hash function, array bit, time complexity and space complexity.
- Let’s look on insertion time for different data set.
-----------------------------------------------------------------------------
|Number of UUIDs | Set Insertion Time(ms) | Bloom Filter Insertion Time(ms) |
-----------------------------------------------------------------------------
|10 <1 71 |
|100 3 17 |
|1, 000 58 84 |
|10, 000 122 272 |
|100, 000 836 556 |
|1, 000, 000 7395 5173 |
------------------------------------------------------------------------------
- Now, Let’s have a look on memory(JVM heap)
--------------------------------------------------------------------------
|Number of UUIDs | Set JVM heap used(MB) | Bloom filter JVM heap used(MB) |
--------------------------------------------------------------------------
|10 <2 0.01 |
|100 <2 0.01 |
|1, 000 3 0.01 |
|10, 000 9 0.02 |
|100, 000 37 0.1 |
|1, 000, 000 264 0.9 |
---------------------------------------------------------------------------
- Bit counts
----------------------------------------------
|Suggested size of Bloom Filter | Bit count |
----------------------------------------------
|10 40 |
|100 378 |
|1, 000 3654 |
|10, 000 36231 |
|100, 000 361992 |
|1, 000, 000 3619846 |
-----------------------------------------------
- Number of Hash Functions used for various false positive probabilities:
-----------------------------------------------
|Suggested FPP of Bloom Filter | Hash Functions|
-----------------------------------------------
|3% 5 |
|1% 7 |
|0.1% 10 |
|0.01% 13 |
|0.001% 17 |
|0.0001% 20 |
------------------------------------------------
Conclusion:
Therefore it can be said that Bloom filter is a good choice in a situation where we have to process large data set with low memory consumption. Also, the more accurate result we want, the number of hash functions has to be increased.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...