BK-Tree | Introduction & Implementation
Last Updated :
26 Dec, 2023
BK-Tree is a data structure used for efficient searching of words that are close to a target word in terms of their Levenshtein distance (or edit distance). It is a tree-like data structure, where each node represents a word and its children represent words that are one edit distance away.
- A BK-Tree is constructed by inserting words into an initially empty tree. Each insertion starts at the root node and progresses down the tree by determining the Levenshtein distance between the word being inserted and the word associated with the current node. If the distance is zero, the word is already in the tree and no further action is taken. If the distance is greater than zero, the word is added as a child of the current node, and the process continues with the next node.
- The search algorithm for a BK-Tree starts at the root node and progresses down the tree based on the Levenshtein distance between the target word and the word associated with each node. If the distance between the target word and the word associated with the current node is greater than the maximum allowed distance, the search can stop because it is guaranteed that no further words with a smaller distance can be found.
BK Tree or Burkhard Keller Tree is a data structure that is used to perform spell check based on the Edit Distance (Levenshtein distance) concept. BK trees are also used for approximate string matching. Various auto-correct features in many software can be implemented based on this data structure.
Pre-requisites : Edit distance Problem
Metric tree
Let’s say we have a dictionary of words and then we have some other words which are to be checked in the dictionary for spelling errors. We need to have a collection of all words in the dictionary which are very close to the given word. For instance, if we are checking the word “ruk” we will have {“truck”,”buck”,”duck”,……}. Therefore, spelling mistakes can be corrected by deleting a character from the word or adding a new character in the word, or replacing the character in the word with an appropriate one. Therefore, we will be using the edit distance as a measure for correctness and matching of the misspelled word from the words in our dictionary.
Now, let’s see the structure of our BK Tree. Like all other trees, BK Tree consists of nodes and edges. The nodes in the BK Tree will represent the individual words in our dictionary and there will be exactly the same number of nodes as the number of words in our dictionary. The edge will contain some integer weight that will tell us about the edit distance from one node to another. Let’s say we have an edge from node u to node v having some edge-weight w, then w is the edit distance required to turn the string u to v.
Consider our dictionary with words: { “help” , “hell” , “hello”}. Therefore, for this dictionary our BK Tree will look like the below one.

Every node in the BK Tree will have exactly one child with same edit-distance. In case, if we encounter some collision for edit-distance while inserting, we will then propagate the insertion process down the children until we find an appropriate parent for the string node.
Every insertion in the BK Tree will start from our root node. Root node can be any word from our dictionary.
For example, let’s add another word “shell” to the above dictionary. Now our Dict[] = {“help” , “hell” , “hello” , “shell”}. It is now evident that “shell” has same edit-distance as “hello” has from the root node “help” i.e 2. Hence, we encounter a collision. Therefore, we deal this collision by recursively doing this insertion process on the pre-existing colliding node.
So, now instead of inserting “shell” at the root node “help“, we will now insert it to the colliding node “hello“. Therefore, now the new node “shell” is added to the tree and it has node “hello” as its parent with the edge-weight of 2(edit-distance). Below pictorial representation describes the BK Tree after this insertion.
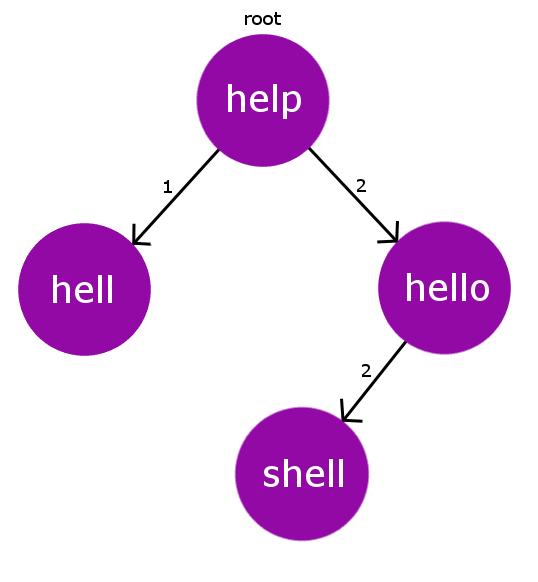
So, till now we have understood how we will build our BK Tree. Now, the question arises that how to find the closest correct word for our misspelled word? First of all, we need to set a tolerance value. This tolerance value is simply the maximum edit distance from our misspelled word to the correct words in our dictionary. So, to find the eligible correct words within the tolerance limit, Naive approach will be to iterate over all the words in the dictionary and collect the words which are within the tolerance limit. But this approach has O(n*m*n) time complexity(n is the number of words in dict[], m is average size of correct word and n is length of misspelled word) which times out for larger size of dictionary.
Therefore, now the BK Tree comes into action. As we know that each node in BK Tree is constructed on basis of edit-distance measure from its parent. Therefore, we will directly be going from root node to specific nodes that lie within the tolerance limit. Lets, say our tolerance limit is TOL and the edit-distance of the current node from the misspelled word is dist. Therefore, now instead of iterating over all its children we will only iterate over its children that have edit distance in range
[dist-TOL , dist+TOL]. This will reduce our complexity by a large extent. We will discuss this in our time complexity analysis.
Consider the below constructed BK Tree.
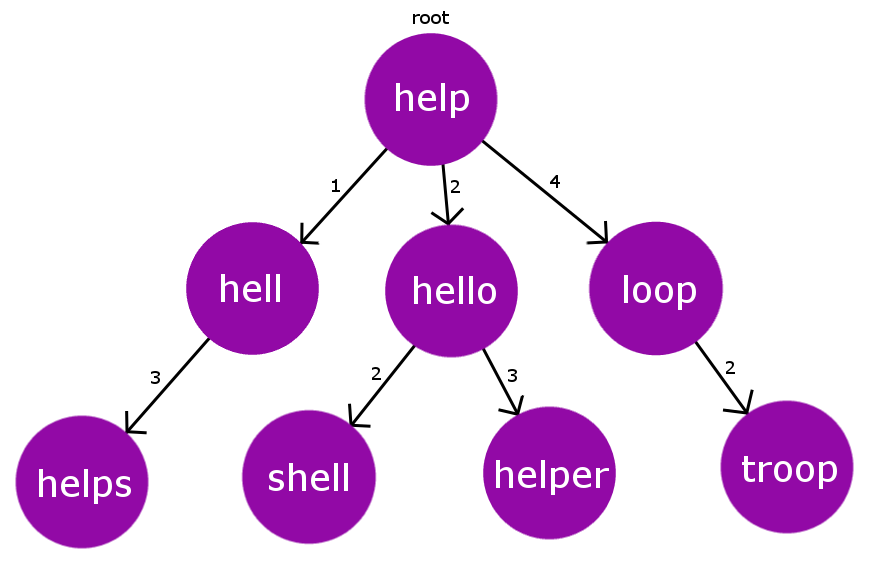
Let’s say we have a misspelled word “oop” and the tolerance limit is 2. Now, we will see how we will collect the expected correct for the given misspelled word.
Iteration 1: We will start checking the edit distance from the root node. D(“oop” -> “help”) = 3. Now we will iterate over its children having edit distance in range [ D-TOL , D+TOL ] i.e [1,5]
Iteration 2: Let’s start iterating from the highest possible edit distance child i.e node “loop” with edit distance 4.Now once again we will find its edit distance from our misspelled word. D(“oop”,”loop”) = 1.
here D = 1 i.e D <= TOL , so we will add “loop” to the expected correct word list and process its child nodes having edit distance in range [D-TOL,D+TOL] i.e [1,3]
Iteration 3: Now, we are at node “troop” . Once again we will check its edit distance from misspelled word. D(“oop”,”troop”)=2 .Here again D <= TOL , hence again we will add “troop” to the expected correct word list.
We will proceed the same for all the words in the range [D-TOL,D+TOL] starting from the root node till the bottom most leaf node. This, is similar to a DFS traversal on a tree, with selectively visiting the child nodes whose edge weight lie in some given range.
Therefore, at the end we will be left with only 2 expected words for the misspelled word “oop” i.e {“loop”, “troop”}
C++
#include "bits/stdc++.h"
using namespace std;
#define MAXN 100
#define TOL 2
#define LEN 10
struct Node
{
string word;
int next[2*LEN];
Node(string x):word(x)
{
for(int i=0; i<2*LEN; i++)
next[i] = 0;
}
Node() {}
};
Node RT;
Node tree[MAXN];
int ptr;
int min(int a, int b, int c)
{
return min(a, min(b, c));
}
int editDistance(string& a,string& b)
{
int m = a.length(), n = b.length();
int dp[m+1][n+1];
for (int i=0; i<=m; i++)
dp[i][0] = i;
for (int j=0; j<=n; j++)
dp[0][j] = j;
for (int i=1; i<=m; i++)
{
for (int j=1; j<=n; j++)
{
if (a[i-1] != b[j-1])
{
dp[i][j] = min( 1 + dp[i-1][j],
1 + dp[i][j-1],
1 + dp[i-1][j-1]
);
}
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
void add(Node& root,Node& curr)
{
if (root.word == "" )
{
root = curr;
return;
}
int dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == "")
{
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else
{
add(tree[root.next[dist]],curr);
}
}
vector <string> getSimilarWords(Node& root,string& s)
{
vector < string > ret;
if (root.word == "")
return ret;
int dist = editDistance(root.word,s);
if (dist <= TOL) ret.push_back(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
vector <string> tmp =
getSimilarWords(tree[root.next[start]],s);
for (auto i : tmp)
ret.push_back(i);
start++;
}
return ret;
}
int main(int argc, char const *argv[])
{
string dictionary[] = {"hell","help","shell","smell",
"fell","felt","oops","pop","oouch","halt"
};
ptr = 0;
int sz = sizeof(dictionary)/sizeof(string);
for(int i=0; i<sz; i++)
{
Node tmp = Node(dictionary[i]);
add(RT,tmp);
}
string w1 = "ops";
string w2 = "helt";
vector < string > match = getSimilarWords(RT,w1);
cout << "similar words in dictionary for : " << w1 << ":\n";
for (auto x : match)
cout << x << endl;
match = getSimilarWords(RT,w2);
cout << "Correct words in dictionary for " << w2 << ":\n";
for (auto x : match)
cout << x << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
class Node {
String word;
int[] next = new int[20];
Node(String x) {
this.word = x;
for (int i = 0; i < 20; i++)
next[i] = 0;
}
Node() {}
}
public class Main {
static final int MAXN = 100;
static final int TOL = 2;
static final int LEN = 10;
static Node RT = new Node();
static Node[] tree = new Node[MAXN];
static int ptr;
public static void main(String[] args) {
String[] dictionary = {"hell", "help", "shell", "smell",
"fell", "felt", "oops", "pop", "oouch", "halt"
};
ptr = 0;
int sz = dictionary.length;
for (int i=0; i<sz; i++) {
Node tmp = new Node(dictionary[i]);
add(RT,tmp);
}
String w1 = "ops";
List<String> match1 = getSimilarWords(RT,w1);
System.out.println("similar words in dictionary for "+w1+" : ");
for (String str : match1)
System.out.print(str+" ");
System.out.println();
String w2= "helt";
List<String> match2= getSimilarWords(RT,w2);
System.out.println("similar words in dictionary for "+w2+" : ");
for (String str : match2)
System.out.print(str+" ");
System.out.println();
}
public static void add(Node root,Node curr) {
if (root.word == null ) {
root.word=curr.word;
root.next=curr.next;
return ;
}
int dist=editDistance(curr.word,root.word);
if(tree[root.next[dist]]==null || tree[root.next[dist]].word==null) {
ptr++;
tree[ptr]=curr;
root.next[dist]=ptr;
}else{
add(tree[root.next[dist]],curr);
}
}
public static List<String> getSimilarWords(Node root,String s){
List<String> ret=new ArrayList<>();
if(root==null || root.word==null)return ret;
int dist=editDistance(root.word,s);
if(dist<=TOL)ret.add(root.word);
int start=dist-TOL;if(start<0)start=1;
while(start<=dist+TOL){
List<String> tmp=getSimilarWords(tree[root.next[start]],s);
ret.addAll(tmp);start++;
}return ret;}
public static int editDistance(String a,String b){
int m=a.length(),n=b.length();
int[][] dp=new int[m+1][n+1];
for(int i=0;i<=m;i++)dp[i][0]=i;for(int j=0;j<=n;j++)dp[0][j]=j;for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(a.charAt(i-1)!=b.charAt(j-1)){
dp[i][j]=Math.min( Math.min( 1 + dp[i-1][j],
1 + dp[i][j-1]),
1 + dp[i-1][j-1]
);
}else{
dp[i][j]=dp[i-1][j-1];
}
}
}return dp[m][n];}
}
|
Python3
import queue
class Node:
def __init__(self, x=None):
self.word = x
self.next = [0] * 20
def add(root, curr):
if not root.word:
root.word = curr.word
root.next = curr.next
return
dist = edit_distance(curr.word, root.word)
if not tree[root.next[dist]] or not tree[root.next[dist]].word:
global ptr
ptr += 1
tree[ptr] = curr
root.next[dist] = ptr
else:
add(tree[root.next[dist]], curr)
def get_similar_words(root, s):
ret = []
if not root or not root.word:
return ret
dist = edit_distance(root.word, s)
if dist <= TOL:
ret.append(root.word)
start = dist - TOL if dist - TOL > 0 else 1
while start <= dist + TOL:
tmp = get_similar_words(tree[root.next[start]], s)
ret += tmp
start += 1
return ret
def edit_distance(a, b):
m, n = len(a), len(b)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m + 1):
dp[i][0] = i
for j in range(n + 1):
dp[0][j] = j
for i in range(1, m + 1):
for j in range(1, n + 1):
if a[i - 1] != b[j - 1]:
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
)
else:
dp[i][j] = dp[i - 1][j - 1]
return dp[m][n]
MAXN = 100
TOL = 2
LEN = 10
RT = Node()
tree = [Node() for _ in range(MAXN)]
ptr = 0
if __name__ == "__main__":
dictionary = ["hell", "help", "shell", "smell", "fell", "felt", "oops", "pop", "oouch", "halt"]
sz = len(dictionary)
for i in range(sz):
tmp = Node(dictionary[i])
add(RT, tmp)
w1 = "ops"
match1 = get_similar_words(RT, w1)
print("similar words in dictionary for", w1, ": ")
for word in match1:
print(word, end=" ")
print()
w2 = "helt"
match2 = get_similar_words(RT, w2)
print("similar words in dictionary for", w2, ": ")
for word in match2:
print(word, end=" ")
print()
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
public class BKTree
{
const int MAXN = 100;
const int TOL = 2;
const int LEN = 10;
public class Node
{
public string word;
public int[] next = new int[2 * LEN];
public Node(string x)
{
word = x;
for (int i = 0; i < 2 * LEN; i++)
next[i] = 0;
}
public Node() { }
}
static Node RT;
static Node[] tree = Enumerable.Range(0, MAXN).Select(_ => new Node()).ToArray();
static int ptr;
static int min(int a, int b, int c)
{
return Math.Min(a, Math.Min(b, c));
}
static int EditDistance(string a, string b)
{
int m = a.Length, n = b.Length;
int[,] dp = new int[m + 1, n + 1];
for (int i = 0; i <= m; i++)
dp[i, 0] = i;
for (int j = 0; j <= n; j++)
dp[0, j] = j;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (a[i - 1] != b[j - 1])
{
dp[i, j] = min(1 + dp[i - 1, j],
1 + dp[i, j - 1],
1 + dp[i - 1, j - 1]
);
}
else
dp[i, j] = dp[i - 1, j - 1];
}
}
return dp[m, n];
}
static void Add(Node root, Node curr)
{
if (string.IsNullOrEmpty(root.word))
{
root.word = curr.word;
return;
}
int dist = EditDistance(curr.word, root.word);
if (string.IsNullOrEmpty(tree[root.next[dist]].word))
{
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else
{
Add(tree[root.next[dist]], curr);
}
}
static List<string> GetSimilarWords(Node root, string s)
{
List<string> ret = new List<string>();
if (string.IsNullOrEmpty(root.word))
return ret;
int dist = EditDistance(root.word, s);
if (dist <= TOL) ret.Add(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
List<string> tmp =
GetSimilarWords(tree[root.next[start]], s);
ret.AddRange(tmp);
start++;
}
return ret;
}
public static void Main(string[] args)
{
string[] dictionary = {"hell", "help", "shell", "smell",
"fell", "felt", "oops", "pop", "oouch", "halt"
};
ptr = 0;
RT = new Node();
int sz = dictionary.Length;
for (int i = 0; i < sz; i++)
{
Node tmp = new Node(dictionary[i]);
Add(RT, tmp);
}
string w1 = "ops";
string w2 = "helt";
List<string> match = GetSimilarWords(RT, w1);
Console.WriteLine("similar words in dictionary for : " + w1 + ":");
foreach (var x in match)
Console.WriteLine(x);
match = GetSimilarWords(RT, w2);
Console.WriteLine("Correct words in dictionary for " + w2 + ":");
foreach (var x in match)
Console.WriteLine(x);
}
}
|
Javascript
let MAXN = 100;
let TOL = 2;
let LEN = 10;
let temp = ["hell", "help", "shell", "fell", "felt"];
class Node
{
constructor(x)
{
this.word = x;
this.next = new Array(2*LEN).fill(0);
}
};
let RT = new Node("");
let tree = new Array(MAXN);
for(let i = 0; i < MAXN; i++){
tree[i] = new Node("");
}
let ptr;
function min(a, b, c)
{
return Math.min(a, Math.min(b, c));
}
function editDistance(a,b)
{
let m = a.length;
let n = b.length;
let dp = new Array(m + 1);
for(let i = 0; i < m + 1; i++){
dp[i] = new Array(n + 1);
}
for (let i=0; i<=m; i++)
dp[i][0] = i;
for (let j=0; j<=n; j++)
dp[0][j] = j;
for (let i=1; i<=m; i++)
{
for (let j=1; j<=n; j++)
{
if (a[i-1] != b[j-1])
{
dp[i][j] = min( 1 + dp[i-1][j],
1 + dp[i][j-1],
1 + dp[i-1][j-1]
);
}
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
function add(root, curr)
{
if (root.word == "" )
{
root = curr;
return root;
}
let dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == "")
{
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else
{
root = add(tree[root.next[dist]],curr);
}
return root;
}
function getSimilarWords(root,s)
{
let ret = new Array();
if (root.word == "")
return ret;
let dist = editDistance(root.word,s);
if (dist <= TOL) ret.push(root.word);
let start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
let tmp = getSimilarWords(tree[root.next[start]],s);
for(let i = 0; i < tmp.length; i++)
ret.push(tmp[i]);
start++;
}
return ret;
}
let dictionary = ["hell","help","shell","smell", "fell","felt","oops","pop","oouch","halt"];
ptr = 0;
let sz = dictionary.length;
for(let i=0; i<sz; i++)
{
let tmp = new Node(dictionary[i]);
RT = add(RT, tmp);
}
let w1 = "ops";
let w2 = "helt";
let match = getSimilarWords(RT,w1);
console.log("similar words in dictionary for : " + w1);
for(let i = 0; i < match.length; i++){
console.log(match[i]);
}
match.splice(0, match.length);
for(let i = 0; i < temp.length; i++) match.push(temp[i]);
match.unshift(getSimilarWords(RT,w2)[0]);
console.log("Correct words in dictionary for " + w2);
for(let i = 0; i < match.length; i++){
console.log(match[i]);
}
|
Output
similar words in dictionary for : ops:
oops
pop
Correct words in dictionary for helt:
hell
help
shell
fell
felt
halt
Time Complexity: It is quite evident that the time complexity majorly depends on the tolerance limit. We will be considering tolerance limit to be 2. Now, roughly estimating, the depth of BK Tree will be log n, where n is the size of dictionary. At every level we are visiting 2 nodes in the tree and perfor
C++
#include "bits/stdc++.h"
using namespace std;
#define MAXN 100
#define TOL 2
#define LEN 10
struct Node
{
string word;
int next[2*LEN];
Node(string x):word(x)
{
for(int i=0; i<2*LEN; i++)
next[i] = 0;
}
Node() {}
};
Node RT;
Node tree[MAXN];
int ptr;
int min(int a, int b, int c)
{
return min(a, min(b, c));
}
int editDistance(string& a,string& b)
{
int m = a.length(), n = b.length();
int dp[m+1][n+1];
for (int i=0; i<=m; i++)
dp[i][0] = i;
for (int j=0; j<=n; j++)
dp[0][j] = j;
for (int i=1; i<=m; i++)
{
for (int j=1; j<=n; j++)
{
if (a[i-1] != b[j-1])
{
dp[i][j] = min( 1 + dp[i-1][j],
1 + dp[i][j-1],
1 + dp[i-1][j-1]
);
}
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
void add(Node& root,Node& curr)
{
if (root.word == "" )
{
root = curr;
return;
}
int dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == "")
{
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else
{
add(tree[root.next[dist]],curr);
}
}
vector <string> getSimilarWords(Node& root,string& s)
{
vector < string > ret;
if (root.word == "")
return ret;
int dist = editDistance(root.word,s);
if (dist <= TOL) ret.push_back(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
vector <string> tmp =
getSimilarWords(tree[root.next[start]],s);
for (auto i : tmp)
ret.push_back(i);
start++;
}
return ret;
}
int main(int argc, char const *argv[])
{
string dictionary[] = {"hell","help","shell","smell",
"fell","felt","oops","pop","oouch","halt"
};
ptr = 0;
int sz = sizeof(dictionary)/sizeof(string);
for(int i=0; i<sz; i++)
{
Node tmp = Node(dictionary[i]);
add(RT,tmp);
}
string w1 = "ops";
string w2 = "helt";
vector < string > match = getSimilarWords(RT,w1);
cout << "similar words in dictionary for : " << w1 << ":\n";
for (auto x : match)
cout << x << endl;
match = getSimilarWords(RT,w2);
cout << "Correct words in dictionary for " << w2 << ":\n";
for (auto x : match)
cout << x << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
public class BKTree {
static final int MAXN = 100;
static final int TOL = 2;
static final int LEN = 10;
static class Node {
String word;
int[] next;
public Node(String x) {
word = x;
next = new int[2 * LEN];
for (int i = 0; i < 2 * LEN; i++)
next[i] = 0;
}
public Node() {
}
}
static Node RT;
static Node[] tree = new Node[MAXN];
static int ptr;
static int min(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
static int editDistance(String a, String b) {
if (a == null || b == null) {
return -1;
}
int m = a.length(), n = b.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++)
dp[i][0] = i;
for (int j = 0; j <= n; j++)
dp[0][j] = j;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (a.charAt(i - 1) != b.charAt(j - 1)) {
dp[i][j] = min(1 + dp[i - 1][j],
1 + dp[i][j - 1],
1 + dp[i - 1][j - 1]
);
} else
dp[i][j] = dp[i - 1][j - 1];
}
}
return dp[m][n];
}
static void add(Node root, Node curr) {
if (root == null) {
RT = curr;
return;
}
if (root.word == null || root.word.isEmpty()) {
root.word = curr.word;
return;
}
int dist = editDistance(curr.word, root.word);
if (root.next == null) {
root.next = new int[2 * LEN];
for (int i = 0; i < 2 * LEN; i++)
root.next[i] = 0;
}
if (tree[root.next[dist]] == null) {
tree[root.next[dist]] = new Node();
}
if (tree[root.next[dist]].word == null || tree[root.next[dist]].word.isEmpty()) {
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
} else {
add(tree[root.next[dist]], curr);
}
}
static List<String> getSimilarWords(Node root, String s) {
List<String> ret = new ArrayList<>();
if (root == null || root.word == null || root.word.isEmpty())
return ret;
int dist = editDistance(root.word, s);
if (dist <= TOL) ret.add(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL) {
List<String> tmp = getSimilarWords(tree[root.next[start]], s);
ret.addAll(tmp);
start++;
}
return ret;
}
public static void main(String[] args) {
String[] dictionary = {"hell", "help", "shell", "smell",
"fell", "felt", "oops", "pop", "oouch", "halt"
};
ptr = 0;
RT = new Node();
int sz = dictionary.length;
for (int i = 0; i < sz; i++) {
Node tmp = new Node(dictionary[i]);
add(RT, tmp);
}
String w1 = "ops";
String w2 = "helt";
List<String> match = getSimilarWords(RT, w1);
System.out.println("Similar words in dictionary for : " + w1 + ":");
for (String x : match)
System.out.println(x);
match = getSimilarWords(RT, w2);
System.out.println("Correct words in dictionary for " + w2 + ":");
for (String x : match)
System.out.println(x);
}
}
|
Python3
import math
import math
MAXN = 100
TOL = 2
LEN = 10
class Node:
def __init__(self, x):
self.word = x
self.next = [0] * (2 * LEN)
RT = Node('')
tree = [Node('') for _ in range(MAXN)]
ptr = 0
def editDistance(a, b):
m, n = len(a), len(b)
dp = [[0 for j in range(n+1)] for i in range(m+1)]
for i in range(m+1):
dp[i][0] = i
for j in range(n+1):
dp[0][j] = j
for i in range(1, m+1):
for j in range(1, n+1):
if a[i-1] != b[j-1]:
dp[i][j] = min(1+dp[i-1][j], 1+dp[i][j-1], 1+dp[i-1][j-1])
else:
dp[i][j] = dp[i-1][j-1]
return dp[m][n]
def add(root, curr):
global ptr
if root.word == '':
root.word = curr.word
return
dist = editDistance(curr.word, root.word)
if tree[root.next[dist]].word == '':
ptr += 1
tree[ptr] = curr
root.next[dist] = ptr
else:
add(tree[root.next[dist]], curr)
def getSimilarWords(root, s):
ret = []
if root.word == '':
return ret
dist = editDistance(root.word, s)
if dist <= TOL:
ret.append(root.word)
start = dist - TOL
if start < 0:
start = 1
while start <= dist + TOL:
tmp = getSimilarWords(tree[root.next[start]], s)
for i in tmp:
ret.append(i)
start += 1
return ret
if __name__ == '__main__':
dictionary = ["hell", "help", "shell", "smell",
"fell", "felt", "oops", "pop", "oouch", "halt"]
sz = len(dictionary)
for i in range(sz):
tmp = Node(dictionary[i])
add(RT, tmp)
w1 = "ops"
w2 = "helt"
match = getSimilarWords(RT, w1)
print("similar words in dictionary for :", w1)
for x in match:
print(x)
match = getSimilarWords(RT, w2)
print("Correct words in dictionary for :", w2)
for x in match:
print(x)
|
C#
using System;
using System.Collections.Generic;
public class BKTree
{
const int MAXN = 100;
const int TOL = 2;
const int LEN = 10;
public class Node
{
public string Word;
public int[] Next;
public Node(string x)
{
Word = x;
Next = new int[2 * LEN];
for (int i = 0; i < 2 * LEN; i++)
Next[i] = 0;
}
public Node() { }
}
static Node RT;
static Node[] tree = new Node[MAXN];
static int ptr;
static int Min(int a, int b, int c)
{
return Math.Min(a, Math.Min(b, c));
}
static int EditDistance(string a, string b)
{
if (a == null || b == null)
{
return -1;
}
int m = a.Length, n = b.Length;
int[,] dp = new int[m + 1, n + 1];
for (int i = 0; i <= m; i++)
dp[i, 0] = i;
for (int j = 0; j <= n; j++)
dp[0, j] = j;
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (a[i - 1] != b[j - 1])
{
dp[i, j] = Min(1 + dp[i - 1, j],
1 + dp[i, j - 1],
1 + dp[i - 1, j - 1]
);
}
else
dp[i, j] = dp[i - 1, j - 1];
}
}
return dp[m, n];
}
static void Add(Node root, Node curr)
{
if (root == null)
{
RT = curr;
return;
}
if (root.Word == null || root.Word == "")
{
root.Word = curr.Word;
return;
}
int dist = EditDistance(curr.Word, root.Word);
if (root.Next == null)
{
root.Next = new int[2 * LEN];
for (int i = 0; i < 2 * LEN; i++)
root.Next[i] = 0;
}
if (tree[root.Next[dist]] == null)
{
tree[root.Next[dist]] = new Node();
}
if (tree[root.Next[dist]].Word == null || tree[root.Next[dist]].Word == "")
{
ptr++;
tree[ptr] = curr;
root.Next[dist] = ptr;
}
else
{
Add(tree[root.Next[dist]], curr);
}
}
static List<string> GetSimilarWords(Node root, string s)
{
List<string> ret = new List<string>();
if (root == null || root.Word == null || root.Word == "")
return ret;
int dist = EditDistance(root.Word, s);
if (dist <= TOL) ret.Add(root.Word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
List<string> tmp = GetSimilarWords(tree[root.Next[start]], s);
ret.AddRange(tmp);
start++;
}
return ret;
}
public static void Main()
{
string[] dictionary = {"hell", "help", "shell", "smell",
"fell", "felt", "oops", "pop", "oouch", "halt"
};
ptr = 0;
RT = new Node();
int sz = dictionary.Length;
for (int i = 0; i < sz; i++)
{
Node tmp = new Node(dictionary[i]);
Add(RT, tmp);
}
string w1 = "ops";
string w2 = "helt";
List<string> match = GetSimilarWords(RT, w1);
Console.WriteLine("Similar words in dictionary for : " + w1 + ":");
foreach (var x in match)
Console.WriteLine(x);
match = GetSimilarWords(RT, w2);
Console.WriteLine("Correct words in dictionary for " + w2 + ":");
foreach (var x in match)
Console.WriteLine(x);
}
}
|
Javascript
const MAXN = 100;
const TOL = 2;
const LEN = 10;
class Node {
constructor(x) {
this.word = x;
this.next = new Array(2 * LEN).fill(0);
}
}
const RT = new Node('');
const tree = new Array(MAXN).fill(null).map(() => new Node(''));
let ptr = 0;
function editDistance(a, b) {
const m = a.length, n = b.length;
const dp = new Array(m + 1).fill(null).map(() => new Array(n + 1).fill(0));
for (let i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (let j = 0; j <= n; j++) {
dp[0][j] = j;
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (a[i-1] !== b[j-1]) {
dp[i][j] = Math.min(1 + dp[i-1][j], 1 + dp[i][j-1], 1 + dp[i-1][j-1]);
} else {
dp[i][j] = dp[i-1][j-1];
}
}
}
return dp[m][n];
}
function add(root, curr) {
if (root.word === '') {
root.word = curr.word;
return;
}
const dist = editDistance(curr.word, root.word);
if (tree[root.next[dist]].word === '') {
ptr += 1;
tree[ptr] = curr;
root.next[dist] = ptr;
} else {
add(tree[root.next[dist]], curr);
}
}
function getSimilarWords(root, s) {
const ret = [];
if (root.word === '') {
return ret;
}
const dist = editDistance(root.word, s);
if (dist <= TOL) {
ret.push(root.word);
}
let start = dist - TOL;
if (start < 0) {
start = 1;
}
while (start <= dist + TOL) {
const tmp = getSimilarWords(tree[root.next[start]], s);
for (const i of tmp) {
ret.push(i);
}
start += 1;
}
return ret;
}
const dictionary = ["hell", "help", "shell", "smell", "fell",
"felt", "oops", "pop", "oouch", "halt"];
const sz = dictionary.length;
for (let i = 0; i < sz; i++) {
const tmp = new Node(dictionary[i]);
add(RT, tmp);
}
const w1 = "ops";
const w2 = "helt";
let match = getSimilarWords(RT, w1);
console.log(`similar words in dictionary for: ${w1}`);
for (const x of match) {
console.log(x);
}
match = getSimilarWords(RT, w2);
console.log(`correct words in dictionary for: ${w2}`);
for (const x of match) {
console.log(x);
}
|
g edit distance calculation. Therefore, our Time Complexity will be O(L1*L2*log n), here L1 is the average length of word in our dictionary and L2 is the length of misspelled. Generally, L1 and L2 will be small.
Auxiliary Space: The space complexity of the above implementation is O(L1*L2) where L1 is the number of words in the dictionary and L2 is the maximum length of the word.
References
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...