Biggest Square that can be inscribed within an Equilateral triangle

Given here is an equilateral triangle of side length a. The task is to find the side of the biggest square that can be inscribed within it.
Examples:

Input: a = 5 
Output: 2.32

Input: a = 7
Output: 3.248

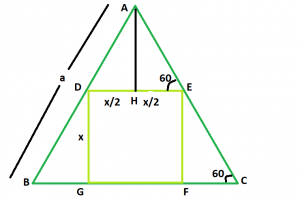
Approach: Let the side of the square be x. 
Now, AH is perpendicular to DE. 
DE is parallel to BC, So, angle AED = angle ACB = 60

In triangle EFC,
              => Sin60 = x/ EC
              => ?3 / 2 = x/EC
              => EC = 2x/?3
In triangle AHE,
              => Cos 60 = x/2AE
              => 1/2 = x/2AE
              => AE = x

So, side AC of the triangle = 2x/?3 + x. Now, 
a = 2x/?3 + x
Therefore, x = a/(1 + 2/?3) = 0.464a
Below is the implementation of the above approach: 

C++

// C++ Program to find the biggest square
// which can be inscribed within the equilateral triangle
#include <bits/stdc++.h>
using namespace std;

// Function to find the side
// of the square
float square(float a)
{

    // the side cannot be negative
    if (a < 0)
        return -1;

    // side of the square
    float x = 0.464 * a;

    return x;
}

// Driver code
int main()
{
    float a = 5;
    cout << square(a) << endl;

    return 0;
}

Java

// Java Program to find the
// the biggest square which
// can be inscribed within
// the equilateral triangle

class GFG
{
    // Function to find the side
    // of the square
    static double square(double a)
    {

        // the side cannot be negative
        if (a < 0)
            return -1;

        // side of the square
        double x = 0.464 * a;
        return x;
    }

    // Driver code
    public static void main(String []args)
    {
        double a = 5;
        System.out.println(square(a));
    }
}

// This code is contributed by ihritik

Python3

# Python3 Program to find the biggest square
# which can be inscribed within the equilateral triangle

# Function to find the side
# of the square
def square( a ):


    # the side cannot be negative
    if (a < 0):
        return -1

    # side of the square
    x = 0.464 * a

    return x


# Driver code
a = 5
print(square(a))

# This code is contributed by ihritik

C#

// C# Program to find the biggest
// square which can be inscribed
// within the equilateral triangle
using System;

class GFG
{
    // Function to find the side
    // of the square
    static double square(double a)
    {

        // the side cannot be negative
        if (a < 0)
            return -1;

        // side of the square
        double x = 0.464 * a;
        return x;
    }

    // Driver code
    public static void Main()
    {
        double a = 5;
        Console.WriteLine(square(a));
    }
}

// This code is contributed by ihritik

PHP

<?php
// PHP Program to find the biggest
//  square which can be inscribed
// within the equilateral triangle

// Function to find the side
// of the square
function square($a )
{

    // the side cannot be negative
    if ($a < 0)
        return -1;

    // side of the square
    $x = 0.464 * $a;
    return $x;
}

// Driver code
$a = 5;
echo square($a);

// This code is contributed by ihritik

?>

Javascript

<script>
// javascript Program to find the
// the biggest square which
// can be inscribed within
// the equilateral triangle


// Function to find the side
// of the square
function square(a)
{

    // the side cannot be negative
    if (a < 0)
        return -1;

    // side of the square
    var x = 0.464 * a;
    return x;
}

// Driver code
    var a = 5;
    document.write(square(a).toFixed(2));

// This code contributed by Princi Singh

</script>

Output:

2.32

Time Complexity: O(1)

Auxiliary Space: O(1)