Bezout’s identity (Bezout’s lemma)
Last Updated :
22 May, 2020
Let a and b be any integer and g be its greatest common divisor of a and b. Then, there exists integers x and y such that ax + by = g …(1).
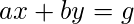
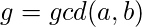
The pair (x, y) satisfying the above equation is not unique. However, all possible solutions can be calculated.
We can find x’ and y’ which satisfies (1) using Euclidean algorithms . All possible solutions of (1) is given by,
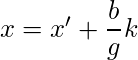
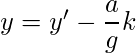
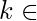
where k is any integer.
It is easy to see why this holds. Just plug in the solutions to (1) to have an intuition.
Also, it is important to see that for general equation of the form,
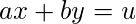
u=gcd(a, b) is the smallest positive integer for which ax+by=u has a solution with integral values of x and y.
Statement: If gcd(a, c)=1 and gcd(b, c)=1, then gcd(ab, c)=1.
Proof:
Above can be easily proved using Bezout’s Identity.
ax+cy=1 and bu+cv=1
Multiply the above two equations,
(ax+cy)(bu+cv)=1
The above implies,
ab(ux)+c(axv+buy+cyv)=1
1 is the only integer dividing L.H.S and R.H.S .
Hence, gcd(ab, c) = 1.
Reference:
https://brilliant.org/wiki/bezouts-identity/
https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...