Beta Distribution in R

Last Updated : 15 Feb, 2022

A distribution in statistics is a function that shows the possible values for a variable and how often they occur in the particular experiment or dataset. Beta distribution is one type of probability distribution that represents all the possible outcomes of the dataset. Beta distribution basically shows the probability of probabilities, where α and β, can take any values which depend on the probability of success/failure.

The general formula for the probability density function of the beta distribution is:

$f(x)=\frac{(x-a)^{p-1}(b-x)^{q-1}}{B(p,q)(b-a)^{p+q-1})}\hspace{.3in} a \le x \le b; p, q > 0.$

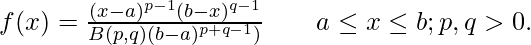
where ,

p and q are the shape parameters
a and b are lower and upper bound
a≤x≤b
p,q>0
B(p,q) is the beta function

To understand the beta distribution in R specifically, we will learn about beta functions. Beta function is a component of beta distribution (the beta function in R can be implemented using the beta (a,b) function) which include these dbeta , pbeta , qbeta , and rbeta which are the functions of the Beta distribution.

Beta function defines as :

$B(\alpha ,\beta )=\int_{0}^{1} t^{^{\alpha -1}}(1-t)^{\beta } dt$

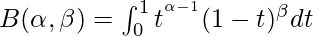
The case where a = 0 and b = 1 is called the standard beta distribution. Hence standard beta distribution is :

$f(x)=\frac{(x)^{p-1}(1-x)^{q-1}}{B(p,q)} \displaystyle \propto {(x)^{p-1}}{(1-x)^{q-1}}\hspace{.3in} 0 \le x \le 1; p, q > 0.$

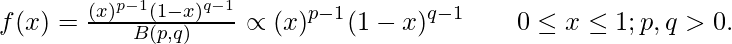
Through beta distribution, we can also find out the measures of central tendency like mean, median mode, and also measures of statistical dispersion like variance.

Why Beta Distribution?

Why we might actually want to choose the beta distribution to specify prior knowledge about theta, one of the major reasons is that this distribution is defined in the range of [0,1] so a beta distribution is a very natural distribution to use when we are talking about probabilities and we want to specify about a prior knowledge of the probabilities of something accruing.

Range of beliefs in Beta Distribution

The range of beliefs is that we can actually define a great set of quite a large range by changing the parameters of p and q i.e. shape parameters.

Let us take an example to understand it better.

S.no.	p	q
1	0.5	0.5
2	0.5	1
3	1	1
4	3	3

Let us start when both p and q are 0.5. We put 1/2 in this equation :

$f(x)={(x)^{p-1}}{(1-x)^{q-1}}\hspace{.3in} 0 \le x \le 1; p, q > 0.$

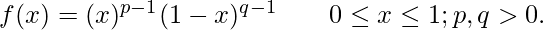
After this it becomes 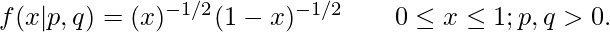$f(x | p,q) = {(x)^{-1/2}(1-x)^{-1/2}}\hspace{.3in} 0 \le x \le 1; p, q > 0.$

then we can also write this equation like :

$f(x |p,q) = \frac {1}{(x)^{1/2}(1-x)^{1/2}}\hspace{.3in} 0 \le x \le 1; p, q > 0.$

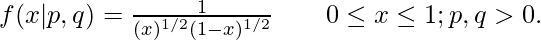
Hence, from the above equation we observed that if x becomes zero or 1 , then we have infinity. Then we will calculate the points for all p and q values. The PDF (Probability distribution function) of Beta distribution can be formed in three shapes from the above observations U-shaped with asymptotic ends, bell-shaped, strictly increasing/decreasing or even straight lines. As you change value of p or q, the shape of the distribution changes.

Hence, the graph will look like this :

Now, let’s plot the Beta distribution functions in R in order to understand them better. Firstly, plot Beta Density and after that all other functions.

Beta density

For plotting the beta density as we know that it will lie between the range of (0,1). We are using one dbeta and plot function in the plot.

Syntax: dbeta(xvalues,alpha,beta)

Example 1: Here, we can observe that Plot for Beta Density(1,1) where we can observe the uniform distribution between 0 and 1.

R

# Creating the Sequence
gfg = seq(0, 1, by = 0.1)
 
# Plotting the beta density
plot(gfg, dbeta(gfg, 1,1), xlab="X",
     ylab = "Beta Density", type = "l",
     col = "Red")

Output:

Plot for Beta Density(1,1)

Example 2: Here, we can observe that Plot for Beta Density(2,1) where we can observe linearly increasing function, In the above plot we can see that is the points are more likely to be near 1 than 0 and they go up in a proportional manner. If we just change the plot from (2,1) to (1,2) we can see that is the points are more likely to be near 0 than 1.

R

# Creating the Sequence
gfg = seq(0,1, by=0.1)
 
# Case 2
plot(gfg, dbeta(gfg, 2,1), xlab="X",
     ylab = "Beta Density", type = "l",
     col = "Red") 

Output:

Plot for Beta Density(2,1)

Example 3: Here, we can observe that Plot for Beta Density(2,2) where we can observe the quadratic function values between nearly 0 and 1 but most likely to have a value near 1/2.

R

# Creating the Sequence
gfg = seq(0,1, by=0.1)
 
# Case 3
plot(gfg, dbeta(gfg, 2,2), xlab = "X",
     ylab = "Beta Density", type = "l",
     col = "Red")

Output:

Plot for Beta Density(2,2)

Cumulative Distributive Functions

You can refer to this link about the functions of Beta Distribution Functions.

Here in our case, the data that we have shows the average which can take any numerical values between 0 and 1 as you can see 0,1 are parameters in sequence in line no.3 in the above code, so through beta distribution, we depict a bounded continuous distribution with values between 0 and 1, and primarily model the uncertainty about the probability of success of a random experiment, which in our case, is the probability of probabilities having a particular average.

Because of this, it is often used in uncertainty problems associated with proportions, frequency or percentages.

R

# The Beta Distribution
plr.data <- data.frame(
  player_avg <- c(seq(0, 1, by = 0.025)),
  stringsAsFactors = FALSE
)
 
# Print the data frame.            
print(plr.data)
print(plr.data$player_avg)
by1 <- dbeta(plr.data$player_avg, shape1 = 5, shape2 = 8)
par(mar = rep(2,4))
plot(by1)
 
# Cummilative distribution function 
by2<- pbeta(plr.data$player_avg, shape1 = 4, shape2 = 6) 
par(mar = rep(2,4))
plot(by2)
 
# Inverse Cummilative distribution function 
by3 <- qbeta(plr.data$player_avg, shape1 = 4, shape2 = 6)
par(mar = rep(2,4))
plot(by3)
 
b4 <- rbeta(plr.data$player_avg, shape1 = 5, shape2 = 8)
par(mar = rep(2,4))
plot(density(b4), main = "Rbeta Plot")